2023年安徽省安庆市桐城中学高考数学一模试卷

一、单项选择题（本大题共8题，每小题5分，共计40分。每小题列出的四个选项中只有一项是最符合题目要求的）

• 1．集合A={x|y=lg（x²-4）}，集合B={y|y=

  x

  2

  -

  2

  x

  -

  3

  }，全集U=R，则（∁_UA）∪B为（　　）

  A．[-2，2]	B．[-2，+∞）
  C．{2}	D．（-∞，2]∪[3，+8）
  组卷：156引用：3难度：0.7

  解析

• 2．设复数z满足条件|z|=1，那么

  |

  z

  +

  3

  +

  i

  |

  取最大值时的复数z为（　　）

  A． 3 2 + 1 2 i

  B．- 3 2 + 1 2 i

  C． 3 2 - 1 2 i

  D．- 3 2 - 1 2 i
  组卷：108引用：1难度：0.6

  解析

• 3．函数f（x）=x²cosx+xsinx的大致图象是（　　）

  A．

  B．

  C．

  D．
  组卷：88引用：4难度：0.7

  解析

• 4．给出下列命题，其中不正确的命题为（　　）
  ①若样本数据x₁，x₂，…，x₁₀的方差为3，则数据2x₁-1，2x₂-1，…，2x₁₀-1的方差为6；
  ②回归方程为

  ̂

  y

  =

  0

  .

  6

  -

  0

  .

  25

  x

  时，变量x与y具有负的线性相关关系；
  ③随机变量X服从正态分布N（3，σ²），P（X≤4）=0.64，则P（2≤X≤3）=0.07；
  ④甲同学所在的某校高三共有5003人，先剔除3人，再按简单随机抽样的方法抽取容量为200的一个样本，则甲被抽到的概率为

  1

  25

  ．

  A．①③④

  B．③④

  C．①②③

  D．①②③④
  组卷：112引用：3难度：0.8

  解析

• 5．命题p：∀x∈R，

  1

  x

  ＞

  0

  ，则￢p为（　　）

  A．∀x∈R， 1 x ≤ 0	B．∃x0∈R， 1 x 0 ≤ 0
  C．∃x0∈R， 1 x 0 ＞ 0	D．∃x0∈R，x0≤0
  组卷：108引用：5难度：0.8

  解析

• 6．某晚会上某歌舞节目的表演者是3个女孩和4个男孩．演出结束后，7个人合影留念，3个人站在前排，4个人站在后排，其中男孩甲、乙要求站在一起，女孩丙不能站在两边，不同站法的种数为（　　）

  A．96

  B．240

  C．288

  D．432
  组卷：117引用：1难度：0.6

  解析

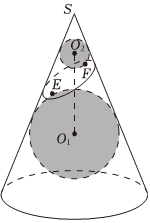• 7．如图是数学家GerminalDandelin用来证明一个平面截圆锥得到的截口曲线是椭圆的模型（称为“Dandelin双球”）；在圆锥内放两个大小不同的小球，使得它们分别与圆锥的侧面、截面相切，设图中球O₁，球O₂的半径分别为4和1，球心距|O₁O₂|=6，截面分别与球O₁，球O₂切于点E，F，（E，F是截口椭圆的焦点），则此椭圆的离心率等于（　　）

  A． 33 9

  B． 6 3

  C． 2 2

  D． 1 6
  组卷：308引用：4难度：0.5

  解析

四、解答题（解答题需写出必要的解题过程或文字说明，17题10分，其余各题每题各12分）

• 21．如图1所示，双曲线具有光学性质：从双曲线右焦点发出的光线经过双曲线镜面反射，其反射光线的反向延长线经过双曲线的左焦点．若双曲线E：

  x

  2

  4

  -

  y

  2

  b

  2

  =1，（b＞0）的左、右焦点分别为F₁，F₂，从F₂发出的光线经过图2中的A，B两点反射后，分别经过点C和D，且，tan∠CAB=-

  3

  4

  ，AB⊥BD．
  （1）求双曲线E的方程；
  （2）设A₁，A₂为双曲线实轴的左右顶点，若过P（4，0）的直线l与双曲线C交于M，N两点，试探究直线A₁M与直线A₂N的交点Q是否在某条定直线上？若存在，请求出该定直线方程；如不存在，请说明理由．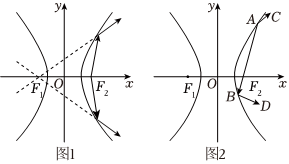
  
  组卷：80引用：1难度：0.4

  解析

• 22．已知函数f（x）=lnx-x,

  g

  （

  x

  ）

  =

  e

  x

  x

  2

  ，其中x＞0．
  （1）分别求函数f（x）和g（x）的极值；
  （2）讨论函数

  h

  （

  x

  ）

  =

  af

  （

  x

  ）

  +

  1

  xg

  （

  x

  ）

  的零点个数．
  组卷：63引用：3难度：0.4

  解析