当前位置：试卷中心 > 试卷详情

2023-2024学年云南师大附中高三（上）期初数学试卷

发布：2024/7/28 8:0:9

1．已知集合M={x|log₂x＜3}，N={x|x＞-1}，则M∩N=（　　）
A．（-1，8） B．（0，8） C．（-1，6） D．（0，6）
组卷：100引用：6难度：0.8
解析
2．已知i是虚数单位，若z₁=2+i,z₂=1+i,则z=z₁•
z
2
在复平面内的对应点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：60引用：7难度：0.9
解析
3．已知曲线y=axe^x+lnx在点（1，ae）处的切线方程为y=3x+b,则（　　）
A．a=e,b=-2 B．a=e,b=2 C．a=e^-1，b=-2 D．a=e^-1，b=2
组卷：518引用：13难度：0.7
解析
4．函数y=（2^x-2^-x）cosx在区间[-2，2]上的图象大致为（　　）
A． B．
C． D．
组卷：134引用：13难度：0.7
解析
5．把语文、数学、英语、物理4本书从左到右排成一行，则语文书和英语书不相邻的概率为（　　）
A．
1
6
B．1 C．
1
2
D．
2
3
组卷：56引用：6难度：0.8
解析
6．如果a＜b＜0，那么下列不等式成立的是（　　）
A．
1
a
＜
1
b
B．ab＜b² C．-ab＜-a² D．
-
1
a
＜
-
1
b
组卷：2899引用：90难度：0.9
解析
7．已知函数f（x）是R上的偶函数，且f（x）的图象关于点（1，0）对称，当x∈[0，1]时，f（x）=2-2^x，则f（0）+f（1）+f（2）+…+f（2022）的值为（　　）
A．-2 B．-1 C．0 D．1
组卷：429引用：11难度：0.7
解析

21．已知函数f（x）=e^x-2ax.
（1）讨论f（x）的单调性；
（2）当a=1时，求函数g（x）=f（x）-cosx在
（
-
π
2
，
+
∞
）
上的零点个数．
组卷：253引用：9难度：0.3
解析
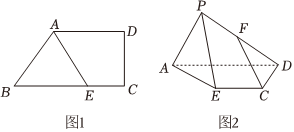22．如图1，在梯形ABCD中，AD∥BC，∠ABC=60°，AB=AD=2，BC=3，点E在线段BC上，BE=2EC，将△ABE沿AE翻折至△PAE的位置，连接PD，点F为PD中点，连接CF，如图2．
（1）在线段AD上是否存在一点Q，使平面PAE∥平面FQC？若存在，请确定点Q的位置，若不存在，请说明理由；
（2）当平面PAE⊥平面AECD时，求三棱锥P-AEF的体积．
组卷：85引用：7难度：0.5
解析

A．	B．
C．	D．

1．已知集合M={x|log2x＜3}，N={x|x＞-1}，则M∩N=（ ）