2022-2023学年辽宁省五校高一（下）期末数学试卷

一、单选题（本大题共8个小题，每小题5分，共40分）

• 1．若

  z

  =

  a

  +

  i

  1

  -

  i

  （

  a

  ∈

  R

  ）

  是纯虚数，则a=（　　）

  A． - 1 2

  B． 1 2

  C．-1

  D．1
  组卷：65引用：5难度：0.8

  解析

• 2．设a=

  1

  2

  cos6°-

  3

  2

  sin6°，b=

  2

  tan

  13

  °

  1

  -

  tan

  2

  13

  °

  ，c=

  1

  -

  cos

  50

  °

  2

  ，则有（　　）

  A．a＞b＞c

  B．a＜b＜c

  C．a＜c＜b

  D．b＜c＜a
  组卷：340引用：16难度：0.7

  解析

• 3．已知向量

  a

  ，

  b

  满足

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  1

  ，

  a

  与

  b

  的夹角为

  π

  4

  ，则

  a

  -

  b

  在

  b

  上的投影向量为（　　）

  A． 2 4 b

  B． 2 2 b

  C． 4 + 2 4 b

  D． - 2 + 2 2 b
  组卷：95引用：1难度：0.8

  解析

• 4．在△ABC中，∠BAC=120°，AD平分∠BAC，AD=3，则2AC+AB的最小值为（　　）

  A． 6 + 3 2

  B． 6 - 3 2

  C． 9 + 6 2

  D． 9 - 6 2
  组卷：250引用：3难度：0.5

  解析

• 5．正四棱锥S-ABCD的底面边长为2，高为2，E是边BC的中点，动点P在表面上运动，并且总保持PE⊥AC，则动点P的轨迹的周长为（　　）

  A． 6 + 2

  B． 6 - 2

  C．4

  D． 5 + 1
  组卷：89引用：2难度：0.5

  解析

• 6．已知底面半径为3的圆锥SO，其轴截面为正三角形，若它的一个内接圆柱的底面半径为1，则此圆柱的侧面积为（　　）

  A． 3 π

  B． 2 3 π

  C． 4 3 π

  D． 8 3 π
  组卷：136引用：2难度：0.5

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  cos

  （

  ωx

  +

  2

  π

  3

  ）

  （

  ω

  ＞

  0

  ）

  在

  [

  -

  π

  ，

  π

  2

  ]

  上单调，且y=f（x）的图象关于点

  （

  -

  π

  3

  ，

  0

  ）

  对称，则（　　）

  A．f（x）的周期为π

  B．若|f（x1）-f（x2）|=2，则|x1-x2|min=2π

  C．将f（x）的图象向右平移 π 3 个单位长度后对应的函数为偶函数

  D．函数 y = f （ x ） + 2 2 在[0，π]上有2个零点
  组卷：94引用：1难度：0.5

  解析

四、解答题（本大题共6个小题，共70分，）

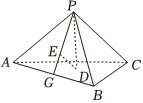• 21．如图，在三棱锥P-ABC中，△ABC是边长为

  6

  2

  的等边三角形，且PA=PB=PC=6，PD⊥平面ABC，垂足为D，DE⊥平面PAB，垂足为E，连接PE并延长交AB于点G．
  （1）求二面角P-AB-C的余弦值；
  （2）在平面PAC内找一点F，使得EF⊥平面PAC，说明作法及理由，并求四面体PDEF的体积．
  组卷：193引用：2难度：0.6

  解析

• 22．已知点O是锐角△ABC的外心，a,b,c分别为角A，B，C的对边，a²=b²+c²-bc,
  （Ⅰ）求角A；
  （Ⅱ）若a=4，求△ABC面积的最大值；
  （Ⅲ）若

  cos

  A

  sin

  C

  BA

  +

  cos

  C

  sin

  A

  BC

  =

  x

  OB

  ，求x的取值范围．
  组卷：84引用：3难度：0.5

  解析