2022-2023学年黑龙江省双鸭山市八年级(下)期末数学试卷
发布:2024/7/7 8:0:9
一、选择题(每题3分,满分30分)
-
1.下列各式计算正确的是( )
组卷:180引用:4难度:0.7 -
2.满足下列条件的△ABC,其中不是直角三角形的是( )
组卷:101引用:5难度:0.5 -
3.某校男子足球队的年龄分布如下表:
则这些队员年龄的平均数是( )年龄/岁 13 14 15 16 17 18 人数 2 6 8 3 2 1 组卷:108引用:6难度:0.5 -
4.在同一平面直角坐标系中,一次函数的y1=ax+b与y2=bx+a图象可能是( )
组卷:389引用:5难度:0.5 -
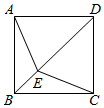 5.如图,在正方形ABCD中,点E是对角线上一点,连接AE,CE,若DE=AB,则∠AEC的度数为( )组卷:399引用:5难度:0.5
5.如图,在正方形ABCD中,点E是对角线上一点,连接AE,CE,若DE=AB,则∠AEC的度数为( )组卷:399引用:5难度:0.5 -
6.我们规定:对于任意的正数m,n的运算“Φ”为当m<n时,mΦn=2
;当m≥n时,mΦn=2m+n,其他运算符号意义不变,按上述规定,计算(3Φ2)-(8Φ12)的结果为( )m-n组卷:336引用:8难度:0.5 -
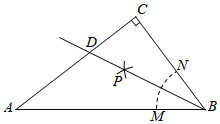 7.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )12组卷:1816引用:34难度:0.7
7.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )12组卷:1816引用:34难度:0.7 -
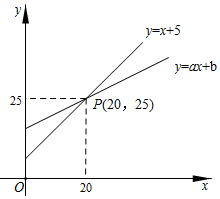 8.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )组卷:4362引用:52难度:0.6
8.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )组卷:4362引用:52难度:0.6
三、解答题(满分66分)
-
25.(1)【感知】如图①,四边形ABCD、CEFG均为正方形.BE与DG的数量关系为.
(2)【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.请判断BE与DG的数量关系,并说明理由
(3)【应用】如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为9,则菱形CEFG的面积为.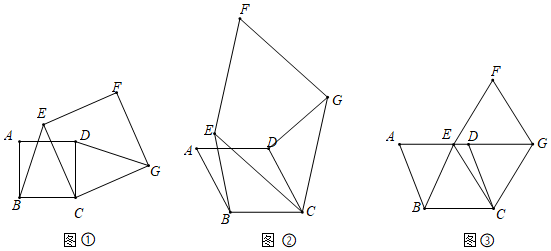 组卷:467引用:8难度:0.3
组卷:467引用:8难度:0.3 -
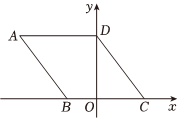 26.如图所示,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(-5,4),点B,C在x轴上,点D在y轴上.
26.如图所示,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(-5,4),点B,C在x轴上,点D在y轴上.
(1)求点B的坐标;
(2)动点P以每秒1个单位长度的速度从点O出发,沿射线OB方向运动,设点P运动的时间为t秒,连接PD,BD,设△PBD的面积为S(S≠0),求S与t的函数关系式(请直接写出自变量t的取值范围);
(3)在(2)的条件下,平面内是否存在点Q,使以A,C,P,Q为顶点的四边形为矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.组卷:110引用:5难度:0.5


