2022-2023学年四川省遂宁市高二（下）期末数学试卷（文科）

一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知i是虚数单位，则复数i（1+i）的共轭复数为（　　）

  A．1+i

  B．1-i

  C．-1+i

  D．-1-i
  组卷：2引用：5难度：0.9

  解析

• 2．命题“∀x＜0，-x²+5x-6＞0”的否定为（　　）

  A．∀x＜0，-x2+5x-6≤0	B．∀x≥0，-x2+5x-6≤0
  C．∃x0＜0， - x 2 0 + 5 x 0 - 6 ≤ 0	D．∃x0≥0， - x 2 0 + 5 x 0 - 6 ≤ 0
  组卷：228引用：4难度：0.8

  解析

• 3．“a+1＞b-2”是a＞b”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：653引用：7难度：0.8

  解析

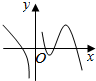• 4．设f（x）在定义域内可导，其图象如图所示，则导函数f′（x）的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：1621引用：26难度：0.9

  解析

• 5．已知抛物线C：y²=20x的焦点为F，抛物线C上有一动点P，Q（6，5），则|PF|+|PQ|的最小值为（　　）

  A．10

  B．16

  C．11

  D．26
  组卷：281引用：5难度：0.7

  解析

• 6．执行如图所示的算法框图，则输出的l的值为（　　）
  

  A．4

  B．5

  C．6

  D．7
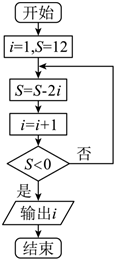  组卷：14引用：4难度：0.7

  解析

• 7．“燃脂单车”运动是一种在音乐的烘托下，运动者根据训练者的指引有节奏的踩踏单车，进而达到燃脂目的的运动，由于其操作简单，燃脂性强，受到广大健身爱好者的喜爱．已知某一单车爱好者的骑行速度v（单位：km/h）随时间t（单位：h）变换的函数关系为

  v

  （

  t

  ）

  =

  2

  t

  e

  t

  +

  15

  ，

  t

  ∈

  [

  1

  2

  ，

  2

  ]

  ，则该单车爱好者骑行速度的最大值为（　　）

  A． 4 e 2 + 15

  B． 2 e 2 + 15

  C． 2 e + 15

  D． 1 e 1 2 + 15
  组卷：31引用：5难度：0.6

  解析

三、解答题（本大题共70分。解答应写出文字说明、证明过程或演算步骤。）[选修4-4：坐标系与参数方程选讲]

• 21．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）与双曲线x²-y²=

  1

  2

  有相同的焦点F₁，F₂，P为椭圆上一点，△PF₁F₂面积最大值为

  3

  ．
  （1）求椭圆C的方程；
  （2）直线y=kx（k≠0）与椭圆C相交于R，S两点，若RE⊥x轴，垂足为E．求证：直线SE的斜率k_SE=

  1

  2

  k；
  （3）A为椭圆C的右顶点，若过点G（3，0）且斜率不为0的直线交椭圆C于M、N两点，O为坐标原点．问：x轴上是否存在定点T，使得∠MTO=∠NTA恒成立．若存在，请求出点T的坐标；若不存在，请说明理由．
  组卷：51引用：1难度：0.3

  解析

• 22．已知函数f（x）=e^x-ax（e是自然对数的底数）．
  （1）当a=1时，求f（x）的极值点；
  （2）讨论函数f（x）的单调性；
  （3）若g（x）=e^x（x-1）-alnx+f（x）有两个零点，求实数a的取值范围．
  组卷：78引用：4难度：0.5

  解析