当前位置：试卷中心 > 试卷详情

2021-2022学年北京市大兴区高二（上）期中数学试卷

发布：2024/7/20 8:0:8

1．已知A（1，1），B（2，0），则直线AB的倾斜角为（　　）
A．
π
6
B．
π
4
C．
3
π
4
D．
5
π
6
组卷：19引用：1难度：0.8
解析
2．点P（-1，2）到直线x=1的距离等于（　　）
A．0 B．1 C．2 D．3
组卷：21引用：2难度：0.8
解析
3．圆x²+y²-2x+4y+3=0的圆心坐标为（　　）
A．（-2，4） B．（2，-4） C．（1，-2） D．（-1，2）
组卷：151引用：13难度：0.9
解析
4．设
a
、
b
、
c
是空间向量，则以下说法中错误的是（　　）
A．
a
、
b
一定共面 B．
a
、
b
、
c
一定不共面
C．
a
•
b
=
b
•
a
D．
a
•
（
b
+
c
）
=
a
•
b
+
a
•
c
组卷：36引用：2难度：0.7
解析
5．已知向量
a
=
（
-
1
，
2
，
3
）
，
b
=
（
1
，-
2
，
x
）
，且
a
∥
b
，则x等于（　　）
A．-6 B．-3 C．3 D．6
组卷：188引用：4难度：0.9
解析
6．已知圆C₁：x²+y²=1与圆C₂：x²+y²-8y+7=0，则圆C₁与圆C₂的位置关系是（　　）
A．相离 B．相交 C．内切 D．外切
组卷：234引用：4难度：0.8
解析
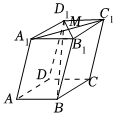7．如图，在平行六面体ABCD-A₁B₁C₁D₁中，M是A₁C₁与B₁D₁的交点，若
A
A
1
=
a
，
AB
=
b
，
AD
=
c
，且
BM
=
x
a
+
y
b
+
z
c
，则x+y+z等于（　　）
A．1 B．
-
1
2
C．0 D．-1
组卷：103引用：8难度：0.8
解析

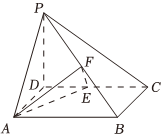20．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD为矩形，E、F分别为CD、PB的中点，AD=PD=2，AB=4．
（1）求点P到平面AEF的距离；
（2）求平面PAD与平面AEF夹角的余弦值．
组卷：42引用：2难度：0.6
解析
21．已知两个定点A（4，0），B（1，0），动点P满足|PA|=2|PB|，设动点P的轨迹为曲线E．
（1）求曲线E的方程；
（2）若Q是直线 l：y=x+4上的动点，过Q作曲线E的两条切线QM，QN，切点分别为M，N，试探究直线MN是否过定点，若过定点请求出定点坐标，若不过定点请说明理由．
组卷：40引用：2难度：0.5
解析

A． a 、 b 一定共面	B． a 、 b 、 c 一定不共面
C． a • b = b • a	D． a • （ b + c ） = a • b + a • c

1．已知A（1，1），B（2，0），则直线AB的倾斜角为（ ）