2020-2021学年浙江省宁波市镇海区立人中学八年级（下）期中数学试卷

一、选择题（共十题：共30分）

• 1．下列图形中，既是中心对称图形又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：16引用：2难度：0.7

  解析

• 2．在下列二次根式中，是最简二次根式的是（　　）

  A． 4

  B． 0 . 8

  C． 1 2

  D． 3 a
  组卷：109引用：2难度：0.7

  解析

• 3．一次数学作业共有10道题目，某小组8位学生做对题目数的情况如下表：
  

  做对题目数	6	7	8	9	10
  人数	1	1	2	3	1

  那么这8位学生做对题目数的众数和中位数分别是（　　）

  A．9和8

  B．9和8.5

  C．3和2

  D．3和1
  组卷：104引用：6难度：0.9

  解析

• 4．已知▱ABCD中，∠A+∠C=200°，则∠B的度数是（　　）

  A．100°

  B．160°

  C．80°

  D．60°
  组卷：1974引用：128难度：0.9

  解析

• 5．一元二次方程x²+3x+5=0的根的情况是（　　）

  A．无实数根	B．有两个不相等的实数根
  C．有两个相等的实数根	D．不能确定
  组卷：535引用：4难度：0.6

  解析

• 6．若n边形的内角和等于外角和的3倍，则边数n为（　　）

  A．n=6

  B．n=7

  C．n=8

  D．n=9
  组卷：3270引用：20难度：0.7

  解析

• 7．用反证法证明命题“在三角形中，至多有一个内角是直角”时，应先假设（　　）

  A．至少有一个内角是直角	B．至少有两个内角是直角
  C．至多有一个内角是直角	D．至多有两个内角是直角
  组卷：969引用：9难度：0.9

  解析

三、解答题（共七题：共66分）

• 22．宾馆有50间房供游客居住，原定价每间房每天190元．当每间房每天定价为180元时，宾馆会住满；当每间房每天的定价每增加10元时，就会空闲一间房（物价部门规定，此类宾馆的入住费用不得超过原定价的1.5倍）．如果有游客居住，宾馆需对居住的每间房每天支出20元的费用．
  （1）如果每间房当天的定价比房间住满时的房价增加x元时，宾馆

  间房有游客居住（用含x的代数式表示）；
  （2）当房价定为多少元时，宾馆当天的利润为9450元？
  组卷：625引用：4难度：0.7

  解析

• 23．如图1，点G是正方形ABCD对角线DB的延长线上任意一点，以线段BG为边作一个正方形BEFG，线段CE和AG相交于点H．
  （1）求证：CE=AG，CE⊥AG；
  （2）若AB=2，BG=1，求CE的长；
  （3）如图2，正方形BEFG绕点B逆时针旋转a（0°＜a＜90°），连接AE、CG，△BCG与△ABE的面积之差是否会发生变化？若不变，请求出△BCG与△ABE的面积之差；若变化，请说明理由．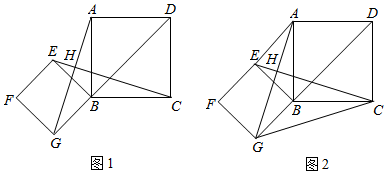
  
  组卷：241引用：3难度：0.1

  解析