2022-2023学年湖北省黄冈市蕲春县英才学校高二（上）期中数学试卷

一、单选题（本大题共8小题，每小题5分，共40分.）

• 1．若直线过两点

  （

  1

  ，

  0

  ）

  ，

  （

  4

  ，

  3

  3

  ）

  ，则此直线的倾斜角是（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  组卷：9引用：2难度：0.7

  解析

• 2．直线2x+（m+1）y-2=0与直线mx+3y-2=0平行，那么m的值是（　　）

  A．2

  B．-3

  C．2或-3

  D．-2或-3
  组卷：335引用：15难度：0.8

  解析

• 3．若动直线l经过点P（1，3），当点Q（3，-3）到直线l的距离最远时，直线l的方程为（　　）

  A．3x+y-6=0

  B．3x+y+6=0

  C．x-3y+8=0

  D．x+3y-10=0
  组卷：150引用：2难度：0.7

  解析

• 4．已知四面体ABCD的所有棱长都等于a,E，F分别是棱AB，CD的中点，则

  EF

  •

  AC

  等于（　　）

  A． - 1 4 a 2

  B． 1 4 a 2

  C． - 1 2 a 2

  D． 1 2 a 2
  组卷：53引用：2难度：0.7

  解析

• 5．圆心为（1，1）且过原点的圆的标准方程是（　　）

  A．（x-1）2+（y-1）2=1	B．（x+1）2+（y+1）2=1
  C．（x+1）2+（y+1）2=2	D．（x-1）2+（y-1）2=2
  组卷：4820引用：72难度：0.9

  解析

• 6．先后抛掷两枚质地均匀的骰子，骰子朝上面的点数分别为a,b,构成一个基本事件（a,b）．记“这些基本事件中，满足log_ba＞1”为事件E，则E发生的概率是（　　）

  A． 5 18

  B． 5 36

  C． 5 12

  D． 1 2
  组卷：94引用：2难度：0.7

  解析

• 7．在一次运动会男子羽毛球单打比赛中，运动员甲和乙进入了决赛．假设每局比赛中甲获胜的概率为0.6，乙获胜的概率为0.4，已知比赛规则是3局2胜制，则乙获得冠军的概率为（　　）

  A．0.288

  B．0.352

  C．0.648

  D．0.256
  组卷：188引用：5难度：0.6

  解析

四、解答题（本大题共6小题，第17题10分，其余各题每题12分，共70分.）

• 21．已知圆C经过点A（1，6）和B（-2，3），且圆心C在直线3x-y=0上．
  （1）求圆C的方程；
  （2）过点P（4，1）作圆C的切线，求切线方程．
  组卷：210引用：9难度：0.7

  解析

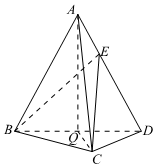• 22．如图，在三棱锥A-BCD中，AB=AD，O为BD的中点，OA⊥CD．
  （1）证明：平面ABD⊥平面BCD；
  （2）若△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，三棱锥B-ACD的体积为

  3

  3

  ，求平面BCD与平面BCE的夹角的余弦值．
  组卷：380引用：8难度：0.5

  解析