当前位置：试卷中心 > 试卷详情

2021-2022学年山西省太原市小店区新时代双语学校九年级（上）月考数学试卷（12月份）

发布：2024/8/27 9:0:9

一、选择题（每小题3分，共30分）

1．如果
a
b
=
2
3
，则
a
+
b
b
等于（　　）
A．1
1
3
B．
1
2
C．
3
5
D．
5
3
组卷：238引用：18难度：0.9
解析
2．用配方法解一元二次方程x²-8x+5=0，将其化成（x+a）²=b的形式，则变形正确的是（　　）
A．（x+4）²=11 B．（x-4）²=21 C．（x-8）²=11 D．（x-4）²=11
组卷：2504引用：38难度：0.7
解析
3．菱形、矩形、正方形都具有的性质是（　　）
A．对角线相等 B．对角线互相垂直
C．对角线互相平分 D．对角线平分一组对角
组卷：450引用：31难度：0.9
解析
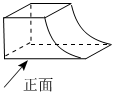4．画如图所示物体的俯视图，正确的是（　　）
A． B． C． D．
组卷：876引用：12难度：0.9
解析
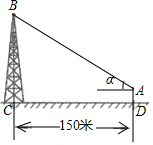5．如图，在离铁塔150米的A处，用测倾仪测得塔顶的仰角为α，测倾仪高AD为1.5米，则铁塔的高BC为（　　）
A．（1.5+150tanα）米 B．（1.5+
150
tanα
）米
C．（1.5+150sinα）米 D．（1.5+
150
sinα
）米
组卷：3010引用：22难度：0.5
解析
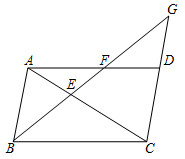6．如图，在平行四边形ABCD中，∠ABC的平分线交AC于点E，交AD于点F，交CD的延长线于点G，若AF=2FD，则
BE
EG
的值为（　　）
A．
1
2
B．
1
3
C．
2
3
D．
3
4
组卷：6723引用：38难度：0.5
解析
7．函数
y
=
k
x
和y=-kx+2（k≠0）在同一平面直角坐标系中的大致图象可能是（　　）
A． B． C． D．
组卷：2529引用：29难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8小题，满分51分）

22．综合与实践：矩形的旋转
问题情境：
在综合与实践课上，老师让同学们以“矩形的旋转”为主题开展数学活动．具体要求：如图1，将长与宽都相等的两个矩形纸片ABCD和EFGH叠放在一起，这时对角线AC和EG互相重合．固定矩形ABCD，将矩形EFGH绕AC的中点O逆时针方向旋转，直到点E与点B重合时停止，在此过程中开展探究活动．
操作发现：
（1）雄鹰小组初步发现：在旋转过程中，当边AB与EF交于点M，边CD与GH交于点N，如图2、图3所示，则线段AM与CN始终存在的数量关系是
．
（2）雄鹰小组继续探究发现：在旋转开始后，当两个矩形纸片重叠部分为四边形QMRN时，如图3所示，四边形QMRN为菱形，请你证明这个结论．
（3）雄鹰小组还发现在问题（2）中的四边形QMRN中∠MQN与旋转角∠AOE存在着特定的数量关系，请你写出这一关系，并说明理由．
实践探究：
（4）在图3中，随着矩形纸片EFGH的旋转，四边形QMRN的面积会发生变化．若矩形纸片的长为
2
+
2
，宽为
2
，请你帮助雄鹰小组探究当旋转角∠AOE为多少度时，四边形QMRN的面积最大？最大面积是多少？（直接写出答案）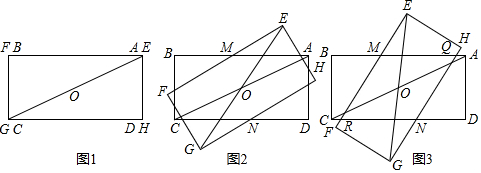
组卷：282引用：2难度：0.1
解析
23．已知，矩形OCBA在平面直角坐标系中的位置如图所示，点C在x轴的正半轴上，点A在y轴的正半轴上，已知点B的坐标为（4，2），反比例函数y=
k
x
的图象经过AB的中点D，且与BC交于点E，设直线DE的解析式为y=mx+n,连接OD，OE．
（1）求反比例函数y=
k
x
的表达式和点E的坐标；
（2）直接写出不等式
k
x
＞mx+n的解集；
（3）点M为y轴正半轴上一点，若△MBO的面积等于△ODE的面积，求点M的坐标；
（4）点P为x轴上一点，点Q为反比例函数y=
k
x
图象上一点，是否存在点P、Q使得以点P，Q，D，E为顶点的四边形为平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．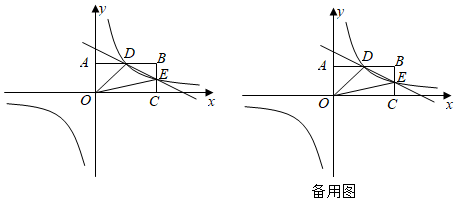
组卷：1209引用：3难度：0.4
解析