2022-2023学年江苏省镇江市四校（扬中二中、句容实验高中等）高一（下）联考数学试卷（5月份）

一、单选题：本大题共8小题，每小题5分，共计40分．在每小题给出的选项中，只有一项符合题目要求，错选或多选得0分．

• 1．平面向量

  a

  与

  b

  的夹角为60°，

  a

  =（2，0），|

  b

  |=1，则|

  a

  +2

  b

  |=（　　）

  A． 3

  B． 2 3

  C．4

  D．12
  组卷：2666引用：143难度：0.9

  解析

• 2．如图所示，一个水平放置的四边形OABC的斜二测画法的直观图是边长为2的正方形O'A'B'C'，则原四边形OABC的面积是（　　）

  A． 16 2

  B． 8 2

  C．16

  D．8
  组卷：407引用：12难度：0.7

  解析

• 3．在△ABC中，已知D是AB边上一点，若

  AD

  =

  2

  DB

  ，

  CD

  =

  1

  3

  CA

  +

  λ

  CB

  ，则λ=（　　）

  A． 2 3

  B． - 2 3

  C． 2 5

  D． 1 3
  组卷：237引用：4难度：0.7

  解析

• 4．欧拉公式e^iθ=cosθ+isinθ把自然对数的底数e、虚数单位 i、三角函数联系在一起，充分体现了数学的和谐美，被誉为“数学中的天桥”，若复数z满足（2e^iπ+i）•z=i,则|z|=（　　）

  A． 1 5

  B． 1 3

  C． 5 5

  D． 3 3
  组卷：25引用：2难度：0.8

  解析

• 5．在△ABC中，内角A，B，C所对应的边分别是a,b,c,若a=3，

  b

  =

  13

  ，B=60°，则c=（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：162引用：3难度：0.8

  解析

• 6．已知正方体AC₁的棱长为1，点P是平面AA₁D₁D的中心，点Q是平面A₁B₁C₁D₁的对角线B₁D₁上一点，且PQ∥平面AA₁B₁B，则线段PQ的长为（　　）

  A． 1 2

  B． 2 2

  C． 2

  D． 3 2
  组卷：21引用：2难度：0.7

  解析

• 7．已知非零向量

  AB

  与

  AC

  满足

  （

  AB

  |

  AB

  |

  +

  AC

  |

  AC

  |

  ）

  •

  BC

  =

  0

  ，且

  AB

  |

  AB

  |

  •

  AC

  |

  AC

  |

  =

  1

  2

  ，则△ABC为（　　）

  A．等边三角形	B．直角三角形
  C．等腰非等边三角形	D．等腰直角三角形
  组卷：142引用：4难度：0.7

  解析

四、解答题：（本大题共6小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤）

• 21．如图，在四棱锥P-ABCD中，PA⊥面ABCD，AB=4，BC=3，AD=5，PA=4，∠DAB=∠ABC=90°，E是CD的中点．
  （1）求异面直线BC与PD所成角的正切值；
  （2）求证：CD⊥PE．
  组卷：658引用：6难度：0.5

  解析

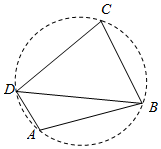• 22．如图，我国南海某处的一个圆形海域上有四个小岛，小岛B与小岛A、小岛C相距都为5 nmile,与小岛D相距为

  3

  5

  nmile

  ．∠BAD为钝角，且

  sin

  A

  =

  3

  5

  ．
  （1）求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积；
  （2）记∠BDC为α，∠CBD为β，求sin（2α+β）的值．
  组卷：348引用：14难度：0.4

  解析