2022-2023学年浙江省台州市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项符合题目要求。

• 1．复数1-2i在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：47引用：3难度：0.9

  解析

• 2．已知向量

  a

  =（1，m），

  b

  =（2，-1），且

  a

  ∥

  b

  ，则m=（　　）

  A． - 1 2

  B． 1 2

  C．2

  D．-2
  组卷：302引用：12难度：0.9

  解析

• 3．我国南宋数学家秦九韶，发现了三角形面积公式，即

  S

  =

  1

  2

  c

  2

  a

  2

  -

  （

  c

  2

  +

  a

  2

  -

  b

  2

  2

  ）

  2

  ，其中a,b,c是三角形的三边，S是三角形的面积．若某三角形三边a,b,c,满足b=1，ca=1，则该三角形面积S的最大值为（　　）

  A． 2 4

  B． 3 4

  C． 2 2

  D． 3 2
  组卷：112引用：2难度：0.8

  解析

• 4．已知表面积为27π的圆锥的侧面展开图是一个半圆，则圆锥的底面半径为（　　）

  A．3

  B． 3 2

  C．6

  D． 4 3
  组卷：88引用：2难度：0.7

  解析

• 5．一个袋子中装有大小和质地相同的5个球，其中有2个黄色球，3个红色球，从袋中不放回的依次随机摸出2个球，则事件“两次都摸到红色球”的概率为（　　）

  A． 1 4

  B． 3 10

  C． 1 3

  D． 1 2
  组卷：71引用：1难度：0.8

  解析

• 6．抛掷一枚骰子5次，记录每次骰子出现的点数，已知这些点数的平均数为2且出现点数6，则这些点数的方差为（　　）

  A．3.5

  B．4

  C．4.5

  D．5
  组卷：67引用：3难度：0.7

  解析

• 7．正三棱台ABC-A₁B₁C₁中，AA₁⊥平面B₁BCC₁，AB=2A₁B₁，则异面直线AB₁与BC₁所成角的余弦值为（　　）

  A． 2 5

  B． 3 5

  C． 4 5

  D． 21 5
  组卷：154引用：4难度：0.4

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．在锐角△ABC中，a,b,c分别为角A，B，C的对边，

  b

  =

  2

  5

  ×

  a

  2

  cos

  C

  -

  c

  2

  cos

  A

  a

  -

  c

  ．
  （1）求证：2b=a+c；
  （2）求sinB的取值范围．
  组卷：145引用：2难度：0.5

  解析

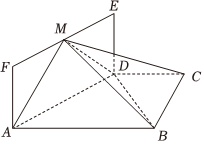• 22．如图，平面ADEF⊥平面ABCD，四边形ADEF为矩形，且M为线段EF上的动点，AB∥CD，∠ABC=90°，AD=2DE，AB=2CD=2BC=2．
  （1）当M为线段EF的中点时，
  （ⅰ）求证：AM⊥平面BDM；
  （ⅱ）求直线AM与平面MBC所成角的正弦值；
  （2）记直线AM与平面MBC所成角为α，平面MAD与平面MBC的夹角为β，是否存在点M使得α=β？若存在，求出FM；若不存在，说明理由．
  组卷：200引用：6难度：0.5

  解析