2022-2023学年北京市延庆区八年级（下）期末数学试卷

一、选择题。（共16分，每小题2分）

• 1．五边形的内角和为（　　）

  A．720°

  B．540°

  C．360°

  D．180°
  组卷：490引用：77难度：0.9

  解析

• 2．如图所示是我国四个银行的行标图案，其中既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：25引用：1难度：0.8

  解析

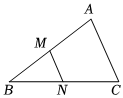• 3．如图，在△ABC中，M，N分别是AB，BC的中点，若MN=3，则AC的长为（　　）

  A．1.5

  B．3

  C．6

  D．9
  组卷：42引用：1难度：0.7

  解析

• 4．函数

  y

  =

  x

  x

  -

  3

  的自变量x的取值范围是（　　）

  A．x=0

  B．x≠0

  C．x=3

  D．x≠3
  组卷：137引用：1难度：0.7

  解析

• 5．用配方法解方程x²-4x=1 时，原方程变形正确的是（　　）

  A．（x+2）2=5

  B．（x-2）2=5

  C．（x+2）2=1

  D．（x-2）2=1
  组卷：141引用：1难度：0.7

  解析

• 6．菱形和平行四边形都具有的性质是（　　）

  A．对角线相等	B．对角线互相垂直
  C．对角线平分一组对角	D．对角线互相平分
  组卷：376引用：3难度：0.5

  解析

• 7．甲、乙两位同学在射击选拔比赛中，各射击了5次，他们的成绩（单位：环）如下表所示：
  

  	第一次	第二次	第三次	第四次	第五次
  甲	8	10	7	7	8
  乙	10	5	10	8	7

  设两人射击成绩的平均数依次为

  x

  _甲，

  x

  _乙，射击成绩的方差依次为S_甲²，S_乙²，则下列关系中完全正确的是（　　）

  A． x 甲 = x 乙 ，S甲2＞S乙2	B． x 甲 = x 乙 ，S甲2＜S乙2
  C． x 甲 ＞ x 乙 ，S甲2＞S乙2	D． x 甲 ＜ x 乙 ，S甲2＜S乙2
  组卷：158引用：3难度：0.6

  解析

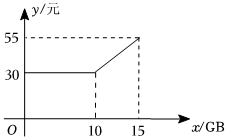• 8．张琳选中某通讯公司的5G极速流量包．已知每月的流量费用y（单位：元）与所用流量x（单位：GB）的函数关系如图所示．则超过套餐内流量后，每GB流量的费用为（　　）

  A．3元

  B．3.7元

  C．5元

  D．55元
  组卷：271引用：3难度：0.8

  解析

二、填空题。（共16分，每小题2分）

• 9．方程x²-3x=0的解是

   

  ．
  组卷：525引用：79难度：0.9

  解析

三、解答题。（共68分，第17题10分，第18-21题，每小题10分，第22题6分，第23-26题，每小题10分，第27题6分，第28题6分）解答应写出文字说明、演算步骤或证明过程.

• 27．如图，AC是正方形ABCD的对角线，点E为射线AB上一个动点，连接CE，以点E为圆心，CE为半径画弧，与直线CA交于点F，连接EF．若∠BCE=α，且0°＜α＜45°．
  （1）如图1，当点E在边AB上时，求∠AEF的度数（用含α的式子表示）；
  （2）如图2，当点E在边AB的延长线上时，
  ①请你依题意补全图形；
  ②用等式表示线段AD，AE，AF之间的数量关系，并证明．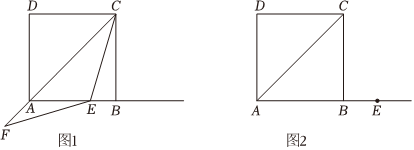
  ​
  组卷：390引用：1难度：0.1

  解析

• 28．在平面直角坐标系xOy中，对于直线l和图形W给出如下定义：若直线l与图形W有且只有一个交点，则称直线l是图形W的“独立关联直线”．
  如图1，直线l是菱形ABCD的“独立关联直线”．
  （1）如图2，点A（1，0），点C（3，1）是矩形ABCD的顶点，若一次函数y=kx-1（k≠0）的图象是这个矩形的“独立关联直线”，求k的值；
  （2）点F，H是直线y=x上的两点，点F的横坐标为a,点H的横坐标为a+1；将正方形EFGH的边HE，EF，FG称为图形M（其中点E的横坐标为a），若直线l：y=-2x+2是图形M的“独立关联直线”，直接写出a的取值范围．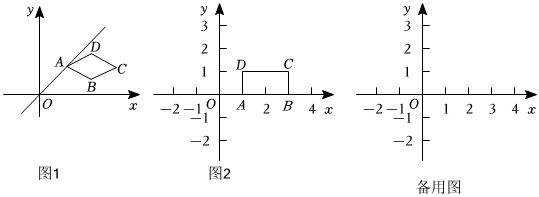
  ​
  组卷：365引用：1难度：0.3

  解析