2023-2024学年北京市昌平区融合学区（第一组）八年级（上）期中数学试卷

一、选择题（共8道小题，每小题2分，共16分）第1-8题均有四个选项，符合题意的选项只有一个.

• 1．16的平方根是（　　）

  A．4

  B．±4

  C．±2

  D．±8
  组卷：356引用：4难度：0.8

  解析

• 2．下列各式中，分式是（　　）

  A． x 2

  B． x π

  C． x x + 1

  D． x 2 + y
  组卷：113引用：2难度：0.9

  解析

• 3．下列分式中最简分式是（　　）

  A． 2 x + 4 6 x + 8	B． x + y x 2 - y 2
  C． x 2 + y 2 x + y	D． x 2 - y 2 x 2 - 2 xy + y 2
  组卷：319引用：2难度：0.6

  解析

• 4．将分式

  3

  x

  x

  -

  y

  中的x,y的值都扩大为原来的2倍，则分式的值（　　）

  A．扩大为原来的2倍	B．扩大为原来的4倍
  C．缩小为原来的一半	D．不变
  组卷：207引用：2难度：0.7

  解析

• 5．若二次根式

  4

  -

  2

  x

  有意义，则x的取值范围是（　　）

  A．x＜2

  B．x≠2

  C．x≤2

  D．x≥2
  组卷：596引用：3难度：0.8

  解析

• 6．下列运算正确的是（　　）

  A． 1 a + 1 b = 1 a + b	B． y x - y - y y - x =0
  C．1÷ b a × a b = a 2 b 2	D． x 2 + y 2 x + y =x+y
  组卷：202引用：1难度：0.6

  解析

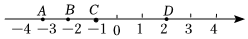• 7．如图，数轴上A，B，C，D四点中，与-

  3

  对应的点距离最近的是（　　）

  A．点A

  B．点B

  C．点C

  D．点D
  组卷：345引用：4难度：0.7

  解析

• 8．生活中有这么一个现象：“糖水加糖就更甜”．设有一杯b克的糖水里含有a克糖，如果在这杯糖水里再加入m克糖（仍不饱和），b＞a＞0，m＞0，则糖水更甜了．根据这一现象，下列不等式正确的是（　　）

  A． a b ＜ a + m b + m

  B． a b ＞ a + m b + m

  C． a b ≤ a + m b + m

  D． a b ≥ a + m b + m
  组卷：592引用：3难度：0.5

  解析

二、填空题（共8道小题，每小题2分，共16分）

• 9．27的立方根为

  ．
  组卷：4688引用：140难度：0.8

  解析

三、解答题（本题共12道小题，第17-22题，每小题5分，第23-26题，每小题5分，第27、28题，每小题5分，共68分）

• 27．对于“分子为1，分母可以写作两个正因数乘积的分数”，可以进行“裂项”转化，
  例如：

  1

  6

  =

  1

  2

  ×

  3

  =

  1

  2

  -

  1

  3

  ；
  

  1

  6

  =

  1

  1

  ×

  6

  =

  1

  5

  ×

  （

  1

  1

  -

  1

  6

  ）

  ；
  

  1

  18

  =

  1

  3

  ×

  6

  =

  1

  3

  ×

  （

  1

  3

  -

  1

  6

  ）

  ；
  

  1

  18

  =

  1

  2

  ×

  9

  =

  1

  7

  ×

  （

  1

  2

  -

  1

  9

  ）

  ；
  …
  参考上面的方法，解决下列问题：
  （1）

  1

  20

  =

  1

  4

  ×

  5

  =

  （

  1

  4

  -

  1

  5

  ）

  ；

  1

  20

  =

  1

  2

  ×

  10

  =

  ×

  （

  1

  2

  -

  1

  10

  ）

  ；
  （2）若将

  1

  15

  裂项变形，则

  1

  15

  =

  ；
  （3）应用上述变形，化简：

  1

  x

  （

  x

  +

  2

  ）

  +

  1

  （

  x

  +

  2

  ）

  （

  x

  +

  4

  ）

  +

  1

  （

  x

  +

  4

  ）

  （

  x

  +

  6

  ）

  +

  …

  +

  1

  （

  x

  +

  2022

  ）

  （

  x

  +

  2024

  ）

  ．
  组卷：161引用：2难度：0.5

  解析

• 28．阅读理解
  材料：为了研究分式

  1

  x

  与分母x的关系，小明制作了表格，并得到如下数据：
  

  x	…	-4	-3	-2	-1	0	1	2	3	4	…
  1 x	…	-0.25	-0. • 3	-0.5	-1	无意义	1	0.5	0. • 3	0.25	…

  从表格数据观察，当x＞0时，随着x的增大，

  1

  x

  的值随之减小，并无限接近0；当x＜0时，随着x的增大，

  1

  x

  的值也随之减小．
  材料2：对于一个分子、分母都是多项式的分式，当分母的次数高于分子的次数时，我们把这个分式叫做真分式．当分母的次数不低于分子的次数时，我们把这个分式叫做假分式．有时候，需要把一个假分式化成整式和真分式的代数和，像这种恒等变形，称为将分式化为部分分式．如：

  2

  x

  +

  1

  x

  -

  4

  =

  2

  x

  -

  8

  +

  8

  +

  1

  x

  -

  4

  =

  2

  x

  -

  8

  x

  -

  4

  +

  8

  +

  1

  x

  -

  4

  =

  2

  +

  9

  x

  -

  4

  ．
  根据上述材料完成下列问题：
  （1）当x＞0时，随着x的增大，

  1

  +

  1

  x

  的值

  （增大或减小）；
  当x＜0时，随着x的增大，

  x

  +

  2

  x

  的值

  （增大或减小）；
  （2）当x＞1时，随着x的增大，

  2

  x

  +

  2

  x

  -

  1

  的值无限接近一个数，请求出这个数；
  （3）当0≤x≤2时，求代数式

  5

  x

  -

  2

  x

  -

  3

  值的范围．
  组卷：1368引用：4难度：0.3

  解析