当前位置：试卷中心 > 试卷详情

2022-2023学年吉林省通化市梅河口五中高二（下）月考数学试卷（3月份）

发布：2024/7/13 8:0:9

一、单选题。本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一个选项是符合题目要求的，请仔细审题，认真做答．

1．已知函数f（x）在x=x₀处的导数为3，则
lim
Δ
x
→
0
f
（
x
0
+
Δ
x
）
-
f
（
x
0
）
2
Δ
x
=（　　）
A．3 B．
3
2
C．6 D．
2
3
组卷：1044引用：18难度：0.7
解析
2．设f（x）=ax³+x,若f'（-1）=4，则a=（　　）
A．1 B．-2 C．3 D．-1
组卷：362引用：11难度：0.8
解析
3．已知等差数列{a_n}的前n项和S_n，若a₂+a₃+a₁₄+a₁₅=40，则S₁₆=（　　）
A．150 B．160
C．170 D．与a₁和公差有关
组卷：505引用：7难度：0.8
解析
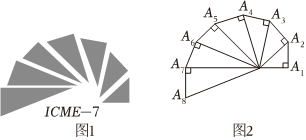
4．图1是第七届国际数学教育大会的会徽图案，会徽的主体图案是由如图2所示的一连串直角三角形演化而成的，其中OA₁=A₁A₂=A₂A₃=…=A₇A₈=1，如果把图2中的直角三角形继续作下去，记OA₁，OA₂，…，OA_n的长度构成的数列为{a_n}，则a₂₅=（　　）
A．25 B．24 C．5 D．4
组卷：53引用：9难度：0.5
解析
5．已知f（x）=
1
4
x
2
+
sin
（
π
2
+
x
）
，f'（x）为f（x）的导函数，则f'（x）的图象是（　　）
A． B．
C． D．
组卷：136引用：8难度：0.7
解析
6．已知数列{a_n}满足
a
2
=
3
，
a
1
=
1
，且
a
2
n
+
1
-
a
2
n
=
2
a
n
-
2
a
n
-
1
+
1
（
n
≥
2
）
，则
a
2
2023
-
2
a
2022
的值为（　　）
A．2021 B．2022 C．2023 D．2024
组卷：82引用：4难度：0.6
解析
7．数列{a_n}的前n项和为S_n，对一切正整数n,点（n,S_n）在函数f（x）=x²+2x的图象上，
b
n
=
2
a
n
+
a
n
+
1
（n∈N^*且n≥1），则数列{b_n}的前n项和为T_n=（　　）
A．
2
n
+
1
-
2
n
-
1
B．
2
n
+
3
-
1
C．
2
n
-
2
n
-
2
D．
2
n
+
3
-
3
组卷：232引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解笿题。本大题共6小题，共70分，请仔细审题，认真做答

21．某林场去年底森林木材储存量为100万m³，若树木以每年20%的增长率生长，计划从今年起，每年底要砍伐x万m³木材，记a_n为第n年年底的木材储存量．
（1）写出a₁，a₂；写出数列{a_n}的递推公式；
（2）为了实现经过10年木材储存量翻两番（原来的4倍）的目标，每年砍伐的木材量x的最大值是多少？（精确到0.1万m³）
参考数据：1.2⁹=5.16，1.2¹⁰=6.19．
组卷：128引用：3难度：0.3
解析
22．已知函数f（x）=lnx+ax²+2（a∈R）．
（1）讨论函数f（x）的单调性；
（2）当a=-1时，证明：函数f（x）有且仅有两个零点x₁，x₂，且
x
1
+
x
2
＞
2
．
组卷：53引用：4难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．150	B．160
C．170	D．与a₁和公差有关

A．	B．
C．	D．

2022-2023学年吉林省通化市梅河口五中高二（下）月考数学试卷（3月份）

一、单选题。本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一个选项是符合题目要求的，请仔细审题，认真做答．

1．已知函数f（x）在x=x0处的导数为3，则limΔx→0f（x0+Δx）-f（x0）2Δx=（ ）

2．设f（x）=ax3+x,若f'（-1）=4，则a=（ ）

3．已知等差数列{an}的前n项和Sn，若a2+a3+a14+a15=40，则S16=（ ）

5．已知f（x）=14x2+sin（π2+x），f'（x）为f（x）的导函数，则f'（x）的图象是（ ）

6．已知数列{an}满足a2=3，a1=1，且a2n+1-a2n=2an-2an-1+1（n≥2），则a22023-2a2022的值为（ ）

7．数列{an}的前n项和为Sn，对一切正整数n,点（n,Sn）在函数f（x）=x2+2x的图象上，bn=2an+an+1（n∈N*且n≥1），则数列{bn}的前n项和为Tn=（ ）

四、解笿题。本大题共6小题，共70分，请仔细审题，认真做答

22．已知函数f（x）=lnx+ax2+2（a∈R）．（1）讨论函数f（x）的单调性；（2）当a=-1时，证明：函数f（x）有且仅有两个零点x1，x2，且x1+x2＞2．

1．已知函数f（x）在x=x₀处的导数为3，则
lim
Δ
x
→
0
f
（
x
0
+
Δ
x
）
-
f
（
x
0
）
2
Δ
x
=（　　）

2．设f（x）=ax³+x,若f'（-1）=4，则a=（　　）

3．已知等差数列{a_n}的前n项和S_n，若a₂+a₃+a₁₄+a₁₅=40，则S₁₆=（　　）

5．已知f（x）=
1
4
x
2
+
sin
（
π
2
+
x
）
，f'（x）为f（x）的导函数，则f'（x）的图象是（　　）

6．已知数列{a_n}满足
a
2
=
3
，
a
1
=
1
，且
a
2
n
+
1
-
a
2
n
=
2
a
n
-
2
a
n
-
1
+
1
（
n
≥
2
）
，则
a
2
2023
-
2
a
2022
的值为（　　）

7．数列{a_n}的前n项和为S_n，对一切正整数n,点（n,S_n）在函数f（x）=x²+2x的图象上，
b
n
=
2
a
n
+
a
n
+
1
（n∈N^*且n≥1），则数列{b_n}的前n项和为T_n=（　　）

22．已知函数f（x）=lnx+ax²+2（a∈R）．
（1）讨论函数f（x）的单调性；
（2）当a=-1时，证明：函数f（x）有且仅有两个零点x₁，x₂，且
x
1
+
x
2
＞
2
．