当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省宁波市余姚中学高一（下）质检数学试卷（3月份）

发布：2024/7/19 8:0:9

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1．已知向量
a
=
（
1
，
k
）
，
b
=
（
2
，
3
）
，
c
=
（
-
2
，
2
）
，且
（
a
-
b
）
⊥
c
，则k=（　　）
A．4 B．-4 C．2 D．-2
组卷：106引用：3难度：0.7
解析
2．若z（1+i）=2-2i（i是虚数单位），则复数z的虚部为（　　）
A．2-2i B．2 C．-2i D．-2
组卷：250引用：3难度：0.8
解析
3．在△ABC中，内角A，B，C所对的边分别为a,b,c,则“
a
b
=
cos
B
cos
A
”是“△ABC是等腰三角形”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：266引用：4难度：0.7
解析
4．已知α为第一象限角，且
tanα
=
4
3
，则
sin
α
2
的值为（　　）
A．
5
5
B．
-
5
5
C．
±
5
5
D．
1
5
组卷：162引用：2难度：0.7
解析
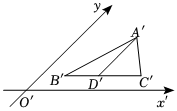5．如图，△A'B'C'是斜二测画法画出的水平放置的△ABC的直观图，D'是B′C′的中点，且A'D'∥y轴，B'C'∥x轴，A'D'=2，B'C'=2，则（　　）
A．BC的长度大于AC的长度 B．△ABC的面积为4
C．△A'B'C'的面积为2 D．
∠
ABC
=
π
3
组卷：230引用：4难度：0.5
解析
6．已知△ABO中，OA=1，OB=2，
OA
•
OB
=
-
1
，过点O作OD垂直AB于点D，则（　　）
A．
OD
=
5
7
OA
+
2
7
OB
B．
OD
=
3
7
OA
+
4
7
OB
C．
OD
=
2
7
OA
+
5
7
OB
D．
OD
=
4
7
OA
+
3
7
OB
组卷：506引用：6难度：0.7
解析
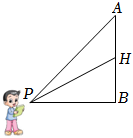7．如图所示，唐唐在背景墙上安装了一台视频监视器，P为唐唐坐在工位上时相当于眼睛位置的一点，P在背景墙上的水平投影点为B，过B作垂直于地面的直线AB，分别交监视器上、下端于A、H两点，测得AB=2m,BH=1.5m,若∠APB=α，∠HPB=β，则α-β为唐唐看监视器的视角．唐唐通过调整工位使视角取得最大值，此时PB的长为（　　）
A．
3
m B．
6
m C．2m D．
4
2
3
m
组卷：174引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本小题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

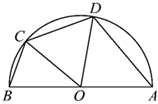21．为了迎接亚运会，滨江区决定改造一个公园，准备在道路AB的一侧建一个四边形花圃种薰衣草（如图）．已知道路AB长为4km,四边形的另外两个顶点C，D设计在以AB为直径的半圆O上．记
∠
COB
=
α
（
0
＜
α
＜
π
2
）
．
（Ⅰ）为了观赏效果，需要保证
∠
COD
=
π
3
，若薰衣草的种植面积不能少于
（
3
+
3
）
km²，则α应设计在什么范围内？
（Ⅱ）若BC=AD，求当α为何值时，四边形ABCD的周长最大，并求出此最大值．
组卷：141引用：4难度：0.6
解析
22．已知函数
f
（
x
）
=
sinxcosx
-
3
co
s
2
x
，将函数f（x）的图象向左平移
π
4
个单位长度，可得到函数g（x）的图象．
（1）求函数g（x）的表达式及单调递增区间；
（2）当
x
∈
[
π
6
，
π
3
]
时，
af
（
x
）
+
g
（
x
）
≥
a
2
+
1
2
-
3
2
（
a
+
1
）
恒成立，求正数a的取值范围．
组卷：29引用：2难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．充分不必要条件	B．必要不充分条件
C．充要条件	D．既不充分也不必要条件

A．BC的长度大于AC的长度	B．△ABC的面积为4
C．△A'B'C'的面积为2	D． ∠ ABC = π 3

A． OD = 5 7 OA + 2 7 OB	B． OD = 3 7 OA + 4 7 OB
C． OD = 2 7 OA + 5 7 OB	D． OD = 4 7 OA + 3 7 OB

2022-2023学年浙江省宁波市余姚中学高一（下）质检数学试卷（3月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1．已知向量a=（1，k），b=（2，3），c=（-2，2），且（a-b）⊥c，则k=（ ）

2．若z（1+i）=2-2i（i是虚数单位），则复数z的虚部为（ ）

3．在△ABC中，内角A，B，C所对的边分别为a,b,c,则“ab=cosBcosA”是“△ABC是等腰三角形”的（ ）

4．已知α为第一象限角，且tanα=43，则sinα2的值为（ ）

5．如图，△A'B'C'是斜二测画法画出的水平放置的△ABC的直观图，D'是B′C′的中点，且A'D'∥y轴，B'C'∥x轴，A'D'=2，B'C'=2，则（ ）

6．已知△ABO中，OA=1，OB=2，OA•OB=-1，过点O作OD垂直AB于点D，则（ ）

四、解答题：本小题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

1．已知向量
a
=
（
1
，
k
）
，
b
=
（
2
，
3
）
，
c
=
（
-
2
，
2
）
，且
（
a
-
b
）
⊥
c
，则k=（　　）

2．若z（1+i）=2-2i（i是虚数单位），则复数z的虚部为（　　）

3．在△ABC中，内角A，B，C所对的边分别为a,b,c,则“
a
b
=
cos
B
cos
A
”是“△ABC是等腰三角形”的（　　）

4．已知α为第一象限角，且
tanα
=
4
3
，则
sin
α
2
的值为（　　）

5．如图，△A'B'C'是斜二测画法画出的水平放置的△ABC的直观图，D'是B′C′的中点，且A'D'∥y轴，B'C'∥x轴，A'D'=2，B'C'=2，则（　　）

6．已知△ABO中，OA=1，OB=2，
OA
•
OB
=
-
1
，过点O作OD垂直AB于点D，则（　　）