2023年宁夏银川市兴庆区景博学校中考数学模拟试卷（二）
发布：2024/6/7 8:0:9
一、选择题（每小题3分，共计24分）
-
1．若
，b=（-1）-1，a=（-32）2，则a,b,c的大小关系是（ ）c=（1-π2）0组卷：347引用：3难度：0.5 -
2．如果直线y=3x+6与y=2x-4交点坐标为（a,b），则
是下列哪个方程组的解（ ）x=ay=b组卷：444引用：8难度：0.6 -
3．某同学对数据26，36，36，46，5■，52进行统计分析发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（ ）
组卷：1473引用：24难度：0.7 -
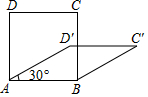4．四边形具有不稳定性，对于四条边长确定的四边形．当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC′D′．若∠D′AB=30°，则菱形ABC′D′的面积与正方形ABCD的面积之比是（ ）组卷：1654引用：21难度：0.9 -
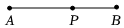5．主持人在舞台上主持节目时，站在黄金分割点上，观众看上去感觉最好．若舞台长30米，主持人从舞台一侧进入，设他至少走x米时恰好站在舞台的黄金分割点上（BP长为x），则x满足的方程是（ ）组卷：454引用：3难度：0.7 -
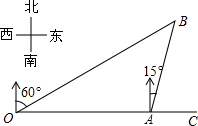6．如图，港口A在观测站O的正东方向，OA=4km,某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（ ）组卷：2686引用：76难度：0.7 -
7．一件工艺品进价为100元，标价130元售出，每天平均可售出100件．根据销售统计，一件工艺品每降价1元出售，则每天可多售出5件，某店为减少库存量，同时使每天平均获得的利润为3000元，每件需降价的钱数为（ ）
组卷：966引用：6难度：0.7 -
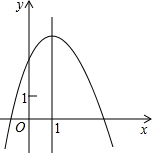8．二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x=1，有如下结论：
①c＜1；
②2a+b=0；
③b2＜4ac；
④若方程ax2+bx+c=0的两根为x1，x2，则x1+x2=2．
则正确的结论是（ ）组卷：1095引用：22难度：0.9
三、解答题（17-22题，每小题6分，23题和24题每小题各8分，25题和26题每小题6分）
-
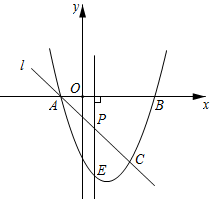25．如图，抛物线y=x2+bx+c与x轴交于A（-1，0），B（3，0）两点，过点A的直线l交抛物线于点C（2，m）．
（1）求抛物线的解析式．
（2）点P是线段AC上一个动点，过点P作x轴的垂线交抛物线于点E，求线段PE最大时点P的坐标．
（3）点F是抛物线上的动点，在x轴上是否存在点D，使得以点A，C，D，F为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点D的坐标；如果不存在，请说明理由．组卷：4739引用：21难度：0.1 -
26．综合与实践
动手实践：数学研究的一个重要内容就是研究变化过程中的不变量．
数学课上张老师拿了两块相似比为1：2的三角板，按图1放置，使60°角的顶点C重合，点D、点E分别在CB、CA边上，∠B=90°，CB=6．将三角板CDE绕点C逆时针旋转，记旋转角为α．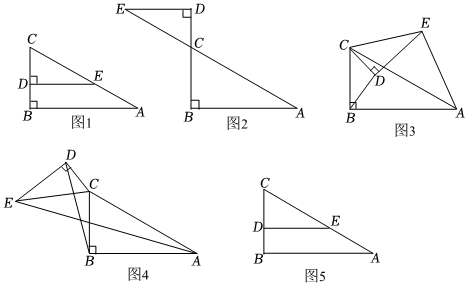
（1）当α=0°时，AE：BD=．
（2）如图2，当α=180°时，AE：BD=．
尝试探究：
（3）猜想：当0°≤α＜360°时，AE：BD的值是否有变化？请选择图3或图4其中一种情况加以证明．
拓展延伸：
（4）如图5，在Rt△ABC中，∠B=90°，AB=4，BC=2，点D、点E分别是边BC、AC的中点，连接DE．将△CDE绕点C逆时针旋转，当旋转至E、B、A三点在同一条直线上时，请你直接写出线段BD的长：BD=．组卷：183引用：2难度：0.5
