2022-2023学年湖北省武汉市东湖高新区八年级（上）期末数学试卷

一、选择题（共10小题．每小题3分，共30分）下列各题中均有四个备选答案，其中有且只有一个是正确的，请在答题卡上将正确答案的代号涂黑．

• 1．下列阿拉伯数字是轴对称图形的是（　　）

  A．6

  B．0

  C．11

  D．69
  组卷：78引用：2难度：0.8

  解析

• 2．若分式

  x

  -

  1

  x

  +

  1

  有意义，则实数x的取值范围是（　　）

  A．x≠1

  B．x≠-1

  C．x=1

  D．x=-1
  组卷：578引用：11难度：0.9

  解析

• 3．0.000000301用科学记数法表示为（　　）

  A．3.01×10-7

  B．3.01×10-6

  C．0.301×10-6

  D．30.1×10-7
  组卷：215引用：3难度：0.8

  解析

• 4．下列运算正确的是（　　）

  A．x3•x-5=x-2	B．（3x）3=9x3
  C．（-a-1b2）3=a-3b6	D． （ b 3 a 2 ） 3 = b 9 a 8
  组卷：376引用：3难度：0.8

  解析

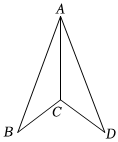• 5．如图，已知∠ACB=∠ACD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（　　）

  A．CB=CD

  B．AC平分∠BAD

  C．AB=AD

  D．∠B=∠D
  组卷：407引用：3难度：0.7

  解析

• 6．

  a

  -

  b

  a

  ÷

  （

  a

  -

  2

  ab

  -

  b

  2

  a

  ）

  计算结果为（　　）

  A． （ a - b ） 3 a 2

  B． 1 a - b

  C．a-b

  D． a - b a
  组卷：1303引用：4难度：0.7

  解析

• 7．下列因式分解正确的是（　　）

  A．a3-a=a（a2-1）

  B．16x2+24x+9=（8x+3）2

  C．25x2-y2=（5x+y）（5x-y）

  D．2m（m+n）+6n（m+n）=（2m+6n）（m+n）（m+n）
  组卷：548引用：4难度：0.8

  解析

• 8．如图，已知△CBE≌△DAE，连接AB、∠ABE=65°，∠BAD=30°，则∠CBE的度数为（　　）

  A．25°

  B．30°

  C．35°

  D．65°
  组卷：858引用：4难度：0.6

  解析

三、解答题（共8小题．共72分）下列各题解答应写出文字说明，证明过程或演算过程

• 23．【问题提出】如图1，在△ABC中，AB=AC，D是BC延长线上的点．连接AD，以AD为边作△ADE（E、D在AC同侧），使DA=DE、∠ADE=∠BAC，连CE．若∠BAC=90°，判断CE与AC的位置关系，并说明理由．
  
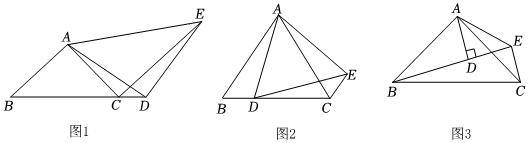
  （1）【问题探究】先将问题特殊化．如图2，当D在线段BC上，∠BAC=60°时，直接写出∠ACE的度数

  ；
  （2）再探究具体情形、如图1，判断CE与AC的位置关系，并说明理由．
  （3）如图3，在△ABC中，AB=AC．点E为△ABC外一点，AD⊥BE于D，∠BEC=∠BAC，DE=3，EC=2．则BD的长为

  ．
  组卷：6引用：4难度：0.1

  解析

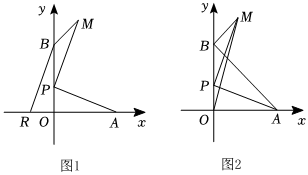• 24．在平面直角坐标系中，点O为坐标原点，A（a,0），B（0，b），且a,b满足（a-4）²+|a-b|=0．
  （1）求点A、点B的坐标．
  （2）P（0，t）为y轴上一动点，连接AP，过点P在线段AP上方作PM⊥PA，且PM=PA．
  ①如图1，若点P在y轴正半轴上，点M在第一象限，连接MB，过点B作PM的平行线交x轴于点R，求点R的坐标（用含t的式子表示）．
  ②如图2，连接OM，探究当OM取最小值时，线段OM与AB的关系．
  组卷：982引用：5难度：0.3

  解析