2023-2024学年江西省吉安市泰和中学高二(上)月考数学试卷(10月份)
发布:2024/9/11 10:0:8
一、单选题(每小题5分)。
-
1.直线l:x+y-3=0的倾斜角为( )
组卷:56引用:4难度:0.9 -
2.已知直线
x+y-1=0与直线23x+my+3=0平行,则它们之间的距离是( )3组卷:1475引用:19难度:0.7 -
3.若点P(1,1)为圆x2+y2-6y=0的弦AB的中点,则弦AB所在直线的方程为( )
组卷:229引用:5难度:0.7 -
4.已知椭圆C:
+x2a2=1(a>b>0)的左、右焦点为F1、F2,离心率为y2b2,过F2的直线l交C于A、B两点,若△AF1B的周长为433,则C的方程为( )3组卷:9030引用:113难度:0.9 -
5.已知圆
与圆C1:(x-a)2+(y+2)2=4相外切,则ab的最大值为( )C2:(x+b)2+(y+1)2=1组卷:141引用:13难度:0.5 -
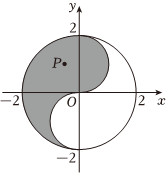 6.“太极图”因其形状如对称的阴阳两鱼互抱在一起,故也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,图中曲线为圆或半圆,已知点P(x,y)是阴影部分(包括边界)的动点,则的最小值为( )yx-2组卷:700引用:42难度:0.7
6.“太极图”因其形状如对称的阴阳两鱼互抱在一起,故也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,图中曲线为圆或半圆,已知点P(x,y)是阴影部分(包括边界)的动点,则的最小值为( )yx-2组卷:700引用:42难度:0.7 -
 7.如图,已知F1,F2分别是椭圆的左、右焦点,现以F2为圆心作一个圆恰好经过椭圆的中心并且交椭圆于点M,N.若过点F1的直线MF1是圆F2的切线,则椭圆的离心率为( )组卷:346引用:13难度:0.6
7.如图,已知F1,F2分别是椭圆的左、右焦点,现以F2为圆心作一个圆恰好经过椭圆的中心并且交椭圆于点M,N.若过点F1的直线MF1是圆F2的切线,则椭圆的离心率为( )组卷:346引用:13难度:0.6
四、解答题
-
21.已知椭圆
+x2a2=1(a>b>0)的焦距为2,点(y2b2,62)在椭圆上.12
(1)求椭圆的方程;
(2)若斜率为1的直线l与椭圆相交于A、B两点,O为原点,求△OAB面积的最大值.组卷:197引用:5难度:0.5 -
22.已知椭圆
的长轴长是短轴长的2倍,且过点B(0,1).x2a2+y2b2=1(a>b>0)
(1)求椭圆的标准方程;
(2)直线l:y=k(x+2)交椭圆于P,Q两点,若点B始终在以PQ为直径的圆内,求实数k的取值范围.组卷:272引用:5难度:0.3


