2022-2023学年北京市丰台区高一(下)期末数学试卷
发布:2024/6/16 8:0:10
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
-
1.已知向量
=(-1,2),a=(-2,k).若b,则实数k=( )a∥b组卷:152引用:1难度:0.7 -
2.设i是虚数单位,则
=( )1-ii组卷:75引用:1难度:0.8 -
3.在平面直角坐标系xOy中,角α与角β均以x轴的非负半轴为始边,终边关于原点O对称.若角α的终边与单位圆⊙O交于点P(
,-23),则cosβ=( )53组卷:216引用:3难度:0.7 -
4.已知sinα=
,α∈(0,45),则π2=( )sin(α-π4)组卷:544引用:7难度:0.8 -
5.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,在该书的第五卷“三斜求积”中,提出了由三角形的三边直接求三角形面积的方法:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”把以上这段文字写成公式,就是
(其中S为三角形面积,a为小斜,b为中斜,c为大斜).在△ABC中,若S=14[c2a2-(c2+a2-b22)2],a=2,c=3,则△ABC的面积等于( )b=3组卷:81引用:1难度:0.8 -
6.已知m,n是两条不重合直线,α,β是两个不重合平面,则下列说法正确的是( )
组卷:189引用:1难度:0.5 -
7.将函数y=cos2x图象上的点
向右平移s(s>0)个单位长度得到点P′.若P′位于函数P(π6,m)的图象上,则( )y=cos(2x-π6)组卷:228引用:2难度:0.5
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
-
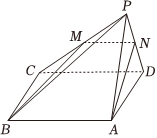 20.如图,在四棱锥P-ABCD中,底面ABCD是矩形,M为棱PC的中点,平面ABM与棱PD交于点N.
20.如图,在四棱锥P-ABCD中,底面ABCD是矩形,M为棱PC的中点,平面ABM与棱PD交于点N.
(Ⅰ)求证:N为棱PD的中点;
(Ⅱ)若平面PAD⊥平面ABCD,AB=4,AD=2,△PAD为等边三角形,求四棱锥P-ABMN的体积.组卷:265引用:1难度:0.6 -
21.设非零向量
=(xk,yk),αk=(yk,-xk)(k∈Ν*),并定义βk.xk+2=αk+1•α1yk+2=βk+1•α1
(Ⅰ)若=(1,2),α1=(3,-2),求|α2|,|α1|,|α2|;α3
(Ⅱ)写出||,|αk|,|αk+1|(k∈Ν*)之间的等量关系,并证明;αk+2
(Ⅲ)若||=|α1|=1,求证:集合{αk|k∈Ν*}是有限集.α2组卷:85引用:1难度:0.5


