2022-2023学年浙江省宁波市镇海区尚志中学七年级(下)期末数学试卷
发布:2024/6/27 8:0:9
一.选择题(每小题3分,共30分)
-
1.下列调查中,最适合采用全面调查方式的是( )
组卷:24引用:1难度:0.9 -
2.冠状病毒的一个变种是非典型肺炎的病原体,某种球形冠状病毒的直径是120纳米,1纳米=10-9米,则这种冠状病毒的半径用科学记数法表示为( )
组卷:1151引用:17难度:0.8 -
3.下列运算正确的是( )
组卷:79引用:1难度:0.9 -
4.使分式
有意义的x的取值范围是( )x-1x+2组卷:93引用:3难度:0.9 -
5.能说明命题“若a2=b2,则a=b”是假命题的一个反例可以是( )
组卷:306引用:3难度:0.5 -
6.下列等式从左到右变形,属于因式分解的是( )
组卷:1199引用:15难度:0.9 -
7.某车间生产一种零件,3位工人生产,1位工人恰好能完成组装,若车间共有工人60人,如何分配工人才能使生产的零件及时组装好.设分配x名工人生产,由题意列方程,下列选项错误的是( )
组卷:409引用:3难度:0.6 -
8.已知关于x,y的方程组
和2x-y=5ax+by=2有相同的解,那么2a+b值是( )x+y=4ax+2by=10组卷:3798引用:12难度:0.6
三.解答题(本大题有8小题,共52分)
-
23.先阅读下面材料,再解决问题:在求多项式的值时,有时可以通过“降次”的方法,把字母的次数从“高次”降为“低次”.一般有“逐步降次法”和“整体代入法”两种做法.例如:已知x2+2x-1=0,求多项式2x2+4x+2021的值.
方法一:∵x2+2x-1=0,∴x2=-2x+1,∴原式=2(-2x+1)+4x+2021=-4x+2+4x+2021=2023.
方法二:∵x2+2x-1=0,∴x2+2x=1,∴原式=2(x2+2x)+2021=2+2021=2023.
(1)应用:已知2x2+6x-3=0,求多项式-3x2-9x+4的值(只需用一种方法即可);
(2)拓展:已知x2+3x-2=0,求多项式3x4+12x3+3x2-6x+5的值(只需用一种方法即可).组卷:676引用:1难度:0.6 -
24.已知,AB∥CD,点E为射线FG上一点.
(1)如图1,若∠EAF=30°,∠EDG=45°,则∠AED=°;
(2)如图2,当点E在FG延长线上时,此时CD与AE交于点H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论:
(3)如图3,DI平分∠EDC,交AE于点K,交AI于点I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°求∠EKD的度数.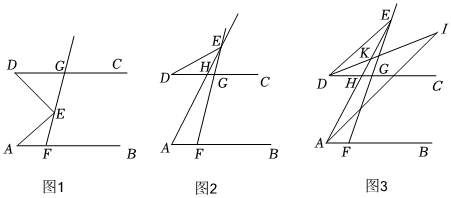 组卷:3051引用:5难度:0.1
组卷:3051引用:5难度:0.1


