2023-2024学年安徽省六安市舒城中学高二（上）开学数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知z（1-i）=3+i（i是虚数单位），z共轭复数为

  z

  ，则

  z

  的虚部为（　　）

  A．2

  B．-2

  C．1

  D．-1
  组卷：37引用：5难度：0.8

  解析

• 2．设a=e^0.7，

  b

  =

  （

  1

  e

  ）

  -

  0

  .

  8

  ，c=log_0.70.8，则a,b,c的大小关系为（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜a＜b
  组卷：130引用：6难度：0.8

  解析

• 3．函数f（x）=

  （

  2

  x

  -

  1

  2

  x

  +

  1

  ）

  sinx在

  [

  -

  3

  π

  2

  ，

  3

  π

  2

  ]

  上的图象的大致形状是（　　）

  A．

  B．

  C．

  D．
  组卷：72引用：7难度：0.7

  解析

• 4．已知log₂（x+y）=log₂x+log₂y,则x+y的最小值是（　　）

  A．1

  B．4

  C．8

  D．16
  组卷：140引用：2难度：0.7

  解析

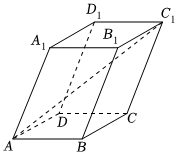• 5．如图，平行六面体ABCD-A₁B₁C₁D₁的底面ABCD是矩形，其中AB=2，AD=4，AA₁=3，且∠A₁AD=∠A₁AB=60°，则线段AC₁的长为（　　）

  A．9

  B． 29

  C． 47

  D． 4 3
  组卷：211引用：9难度：0.5

  解析

• 6．在外接圆半径为

  1

  2

  的△ABC中，a,b,c分别为内角A，B，C的对边，且2asinA=（2b+c）sinB+（2c+b）sinC，则b+c的最大值是（　　）

  A． 1 2

  B．1

  C．3

  D． 3 2
  组卷：137引用：3难度：0.6

  解析

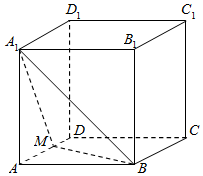• 7．如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，点M是AD的中点，动点P在底面ABCD内（不包括边界）．若B₁P∥平面A₁BM，则C₁P的最小值是（　　）

  A． 30 5

  B． 2 30 5

  C． 2 7 5

  D． 4 7 5
  组卷：380引用：8难度：0.6

  解析

四、解答题（本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤）

• 21．为了普及垃圾分类知识，某校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为p,乙同学答对每题的概率都为q（p＞q），且在考试中每人各题答题结果互不影响，已知每题甲、乙两人同时答对的概率为

  1

  2

  、恰有一人答对的概率为

  5

  12

  ．
  （1）求p和q的值；
  （2）为求甲、乙两人共答对3道题的概率．
  组卷：268引用：12难度：0.8

  解析

• 22．如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC=2BC，E为AB的中点，沿DE将△ADE折起，使得点A到点P的位置，且PE⊥EB，M为PB的中点，N是BC上的动点（与点B、C不重合）．
  
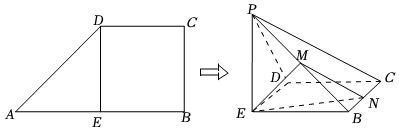
  （1）证明：平面EMN⊥平面PBC；
  （2）是否存在点N，使得二面角B-EN-M的正切值为

  17

  ？若存在，确定N点的位置；若不存在，请说明理由．
  组卷：110引用：3难度：0.4

  解析