当前位置：试卷中心 > 试卷详情

2022-2023学年河北省沧州市重点高中联考高一（下）期中数学试卷

发布：2024/7/20 8:0:8

一、单选题（本大题共8小题，每小题5分，共40分）

1．若复数z=3-2i,则复数z的虚部为（　　）
A．-2i B．2i C．-2 D．2
组卷：71引用：8难度：0.8
解析
2．若A（1，m），B（m+1，3），C（1-m,7）三点共线，则m=（　　）
A．-5 B．5 C．0或-5 D．0或5
组卷：266引用：8难度：0.7
解析
3．已知平面α，β和直线a,b,α∩β=a,b⊂β，则“
a
⊥
b
”是“α⊥β”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：38引用：2难度：0.5
解析
4．某实验室的笼子中有40只小白鼠，将其进行编号，分别为00，01，02，…，39，现从中抽取一个容量为10的样本进行试验，选取方法是从下面的随机数表的第1行第15列和第16列数字开始由左向右依次选取2个数字，直到取足样本，则抽取样本的第6个号码为（　　）
90 84 60 79 80 24 36 59 87 38 82 07 53 89 35 96 35 23 79 18 05 98 90
07 35 46 40 62 98 80 54 97 20 56 95 15 74 80 08 32 16 46 70 50 80 67
A．05 B．40 C．35 D．23
组卷：118引用：2难度：0.8
解析
5．已知（cosx+isinx）ⁿ=cosnx+isinnx（其中i为虚数单位），那么复数
（
cos
π
5
+
isin
π
5
）
2023
在复平面内所对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：24引用：2难度：0.7
解析
6．已知三棱锥P-ABC，PA⊥底面ABC，PA=AC=2，AB=1，
∠
ACB
=
π
6
，则三棱锥P-ABC外接球的体积为（　　）
A．
8
2
π
3
B．
32
π
3
C．
64
2
π
3
D．8π
组卷：105引用：3难度：0.7
解析
7．在△ABC中，点D是边BC的中点，且
AD
=
3
，若点P为平面ABC内一点，则
PA
•
（
PB
+
PC
）
的最小值是（　　）
A．
-
3
2
B．
-
3
2
C．
-
3
4
D．
-
3
4
组卷：36引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分）

21．在△ABC中，内角A，B，C所对的边分别为a,b,c,且满足b（1+2cosA）=c.
（1）证明：A=2B．
（2）求
b
+
3
c
bcos
B
的取值范围．
组卷：46引用：2难度：0.5
解析
22．如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC=2BC，E为AB的中点，沿DE将△ADE折起，使得点A到点P的位置，且PE⊥EB，M为PB的中点，N是BC上的动点（与点B、C不重合）．

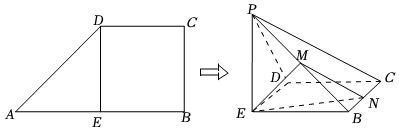
（1）证明：平面EMN⊥平面PBC；
（2）是否存在点N，使得二面角B-EN-M的正切值为
17
？若存在，确定N点的位置；若不存在，请说明理由．
组卷：115引用：3难度：0.4
解析