2022-2023学年湖南省长沙市岳麓区周南梅溪湖中学八年级(上)第三次月考数学试卷
发布:2024/8/20 19:0:2
一、选择题(本大题共12小题,每小题3分,共36分)
-
1.有长分别为2cm,3cm,4cm,5cm的四根木棍,用其中的三根首尾顺次相接不能组成三角形的是( )
组卷:50引用:2难度:0.6 -
2.下列运算正确的是( )
组卷:269引用:7难度:0.7 -
3.把0.000000125这个数据用科学记数法可表示为( )
组卷:250引用:8难度:0.8 -
4.下列式子:-5x,
,1a+b,12a2-12b2,310m,其中分式有( )2π组卷:1302引用:14难度:0.8 -
5.已知钝角三角形ABC,画BC边上的高,正确的画法是( )
组卷:146引用:3难度:0.8 -
6.根据分式的基本性质,分式
可变形为( )-aa-b组卷:1963引用:17难度:0.9 -
7.下列各式变形中,是因式分解的是( )
组卷:3860引用:44难度:0.9 -
8.如果把分式
中的x和y都扩大2倍,那么分式的值( )2xyx+y组卷:1043引用:15难度:0.9
三、解答案题(本大题共8个小题,共66分)
-
25.我们定义:若一条线段将三角形分割成2个等腰三角形,则这条线段是这个三角形的“黄金线”.若两条线段将一个三角形分割成3个等腰三角形,则这两条线段是这个三角形的“钻石线”.例如:如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,过点C作∠ACD=30°,△ACD和△BCD都是等腰三角形,则线段CD是△ABC的“黄金线”.延长CB至点E,使AB=BE,连接AE,两条线段AB、CD将△ACE分割成3个等腰三角形,则这两条线段AB、CD是△ACE的“钻石线”.
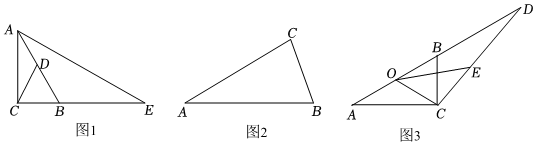
(1)如图2,已知锐角△ABC中,∠BAC=25°,∠ABC=75°,若存在线段BD是△ABC的“黄金线”,则其中钝角等腰三角形的顶角是 °;
(2)如图3,已知△ABC中,∠ACB=90°,∠A=30°,点O是AB的中点,过点C作∠BCD=40°,交AB的延长线于点D,CD边上的一点E恰好在OD的垂直平分线上,求证:线段CO、OE是△ACD的“钻石线”;
(3)若一个等腰三角形有“黄金线”,则这个等腰三角形的底角度数是 °.组卷:454引用:3难度:0.1 -
26.如图,等腰Rt△ABC中,∠ABC=90°,点A、B分别在坐标轴上.
(1)如图①,若C点的横坐标为5,求B点的坐标;
(2)如图②,若x轴恰好平分∠BAC,BC交x轴于点M,过C点作CD⊥x轴于D点,求的值;CDAM
(3)如图③,若点A的坐标为(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于P点,当点B在y轴上移动时,PB的长度是否发生改变?若不变,求出PB的值,若变化,求PB的取值范围.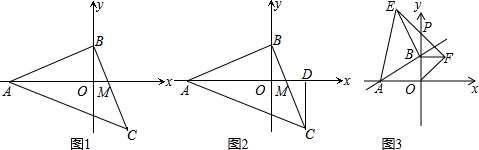 组卷:264引用:4难度:0.9
组卷:264引用:4难度:0.9


