2023-2024学年河南省焦作市博爱一中高二(上)第一次半月考数学试卷
发布:2025/11/24 16:1:2
一、选择题(每小题5分,共8小题40分)
-
1.已知圆C:(x-1)2+(y-2)2=25,则圆C被y轴所截得弦长为( )
组卷:109引用:2难度:0.7 -
 2.中国古代桥梁的建筑艺术,有不少是世界桥梁史上的创举,充分显示了中国劳动人民的非凡智慧.一个抛物线型拱桥,当水面离拱顶2m时,水面宽8m.若水面下降1m,则水面宽度为( )组卷:759引用:5难度:0.8
2.中国古代桥梁的建筑艺术,有不少是世界桥梁史上的创举,充分显示了中国劳动人民的非凡智慧.一个抛物线型拱桥,当水面离拱顶2m时,水面宽8m.若水面下降1m,则水面宽度为( )组卷:759引用:5难度:0.8 -
3.已知椭圆
=1(a1>b1>0)的离心率为x2a21+y2b21,双曲线22=1(a2>0,b2>0)与椭圆有相同的焦点F1,F2,M是两曲线的一个公共点,若∠F1MF2=60°,则双曲线的渐近线方程为( )x2a22-y2b22组卷:184引用:6难度:0.7 -
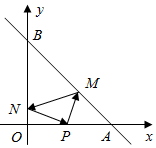 4.如图,已知两点A(4,0),B(0,4),从点P(2,0)射出的光线经直线AB反射后射到直线OB上,再经直线OB反射后射到P点,则光线所经过的路程PM+MN+NP等于( )组卷:815引用:10难度:0.5
4.如图,已知两点A(4,0),B(0,4),从点P(2,0)射出的光线经直线AB反射后射到直线OB上,再经直线OB反射后射到P点,则光线所经过的路程PM+MN+NP等于( )组卷:815引用:10难度:0.5 -
5.过点P(2,-2)且平行于直线2x+y+1=0的直线方程为( )
组卷:2146引用:3难度:0.8 -
6.已知椭圆
的长轴长为4,焦距为2,则( )x2a2+y2b2=1(a>b>0)组卷:88引用:1难度:0.7 -
7.已知第一象限内的点M既在双曲线
的渐近线上,又在抛物线C1:x2a2-y2b2=1(a>0,b>0)上,设C1的左、右焦点分别为F1,F2,若C2的焦点为F2,且△MF1F2是以MF1为底边的等腰三角形,则双曲线的离心率为( )C2:y2=2px(p>0)组卷:717引用:5难度:0.7 -
8.已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,则直线l的斜率k的取值范围是( )
组卷:2195引用:23难度:0.9
二、多选题(每小题5分,共4小题20分)
-
9.已知点P(1,a)(a>1)在抛物线C:y2=2px(p>0)上,过P作圆(x-1)2+y2=1的两条切线,分别交C于A,B两点,且直线AB的斜率为-1,若F为C的焦点,M(x,y)为C上的动点,N是C的准线与坐标轴的交点,则( )
组卷:159引用:3难度:0.2 -
10.下列说法错误的是( )
组卷:124引用:3难度:0.6 -
11.瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上,这条直线被后人称为三角形的“欧拉线”.若△ABC满足AC=BC,顶点A(1,0),B(-1,2),且其“欧拉线”与圆M:(x-3)2+y2=r2相切,则下列结论正确的是( )
组卷:611引用:13难度:0.4 -
12.设点A(-2,3),B(3,2),则下列a的值满足直线ax+y+2=0与线段AB有交点的是( )
组卷:57引用:5难度:0.8
三、填空题(每小题5分,共4小题20分)
-
13.若圆C以椭圆
的右焦点为圆心、长半轴为半径,则圆C的方程为.x216+y212=1组卷:390引用:2难度:0.8 -
14.已知抛物线C:y2=2px(p>0)的焦点为F,点P(6,t)在抛物线C上,且|PF|=9,则p=.
组卷:17引用:2难度:0.7 -
15.已知平面向量
,则实数m=.a=(m,2),b=(1,m),(a+b)•a=|b|2组卷:17引用:2难度:0.8 -
16.直线3x+4y+12=0在x轴上的截距为 .
组卷:55引用:2难度:0.8
四、解答题(第17题10分,第18,19、20、21、22题各12分,共6小题70分)
-
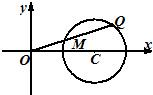 17.如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点,试求点M的轨迹方程.组卷:29引用:2难度:0.3
17.如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点,试求点M的轨迹方程.组卷:29引用:2难度:0.3 -
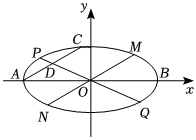 18.如图,已知椭圆的左、右顶点分别为A,B,点C是椭圆上异于A,B的动点,过原点O平行于AC的直线与椭圆交于点M,N,AC的中点为点D,直线OD与椭圆交于点P,Q,点P,C,M在x轴的上方.x24+y2=1
18.如图,已知椭圆的左、右顶点分别为A,B,点C是椭圆上异于A,B的动点,过原点O平行于AC的直线与椭圆交于点M,N,AC的中点为点D,直线OD与椭圆交于点P,Q,点P,C,M在x轴的上方.x24+y2=1
(1)当时,求cos∠POM;|AC|=5
(2)求|PQ|•|MN|的最大值.组卷:139引用:3难度:0.5 -
19.在平面直角坐标系中,已知双曲线I:
,A,B分别为I的左,右顶点.x24-y25=1
(1)以A为圆心的圆与I恰有三个不同的公共点,写出此圆的方程;
(2)直线L过点A,与I在第一象限有公共点P,线段AP的垂直平分线过点B,求直线L的方程;
(3)I上是否存在异于A、B点M、N,使+2MA=MB成立,若存在,求出所有M、N的坐标,若不存在说明理由.MN组卷:408引用:2难度:0.5 -
20.已知三条直线l1:2x-y+a=0(a>0),直线l2:-4x+2y-1=0和l3:x+y+3=0,且l1与l2间的距离是
52
(1)求a的值;
(2)求经过直线l1与l3的交点,且与点(1,3)距离为3的直线l的方程.组卷:880引用:4难度:0.1 -
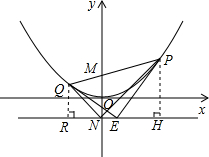 21.已知点M,N的坐标分别是(0,2)和(0,-2),点P是二次函数的图象上的一个动点.y=18x2
21.已知点M,N的坐标分别是(0,2)和(0,-2),点P是二次函数的图象上的一个动点.y=18x2
(1)判断以点P为圆心,PM为半径的圆与直线y=-2的位置关系,并说明理由;
(2)设直线PM与二次函数的图象的另一个交点为Q,连接NP,NQ,求证:∠PNM=∠QNM;y=18x2
(3)过点P,Q分别作直线y=-2的垂线,垂足分别为H,R,取RH中点为E,求证:QE⊥PE.组卷:12引用:1难度:0.1 -
22.已知直线l:y=k(x+2
)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.2
(Ⅰ)试将S表示成的函数S(k),并求出它的定义域;
(Ⅱ)求S的最大值,并求取得最大值时k的值.组卷:692引用:17难度:0.5


