2022-2023学年湖北省黄石市阳新县七年级（下）抽测数学试卷

一.选择题（共6小题，满分36分，每小题6分）

• 1．下列命题：
  ①

  a

  （a≥0）表示a的平方根；
  ②立方根等于本身的数是0；
  ③若ab=0，则P（a,b）在坐标原点；
  ④在平面直角坐标系中，若点A的坐标为（-1，-2），且AB平行于x轴，AB=5，则点B的坐标为（4，-2），
  其中真命题的个数为（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：384引用：4难度：0.5

  解析

• 2．方程组

  a 1 x + b 1 y = c 1

  a 2 x + b 2 y = c 2

  的解为

  x = 8

  y = 3

  ，则方程组

  4 a 1 x + 3 b 1 y = 5 c 1

  4 a 2 x + 3 b 2 y = 5 c 2

  的解为（　　）

  A． x = 8 y = 3

  B． x = 5 y = 4

  C． x = 10 y = 5

  D． x = 10 y = 10
  组卷：368引用：2难度：0.5

  解析

• 3．设

  S

  1

  =

  1

  +

  1

  1

  2

  +

  1

  2

  2

  ，

  S

  2

  =

  1

  +

  1

  2

  2

  +

  1

  3

  2

  ，

  S

  3

  =

  1

  +

  1

  3

  2

  +

  1

  4

  2

  ，…，

  S

  n

  =

  1

  +

  1

  n

  2

  +

  1

  （

  n

  +

  1

  ）

  2

  ，则

  S

  1

  +

  S

  2

  +

  …

  +

  S

  14

  的值为（　　）

  A． 624 25

  B． 14 5

  C． 14 15

  D． 224 15
  组卷：236引用：1难度：0.5

  解析

• 4．关于x的不等式组

  x - t 4 ＜ 0

  x - 5 2 ＜ 3 x 4 - 2

  只有两个整数解，且21t=2a+12，要使

  |

  a

  |

  -

  3

  的值是整数，则符合条件的a个数是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：2210引用：3难度：0.2

  解析

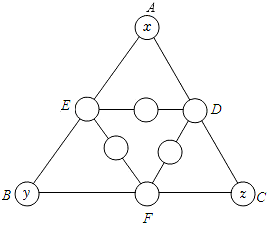• 5．三角形然幻方是锻炼思维的有趣数学问题，例：把数字1、2、3、…、9分别填入如图所示的9个圆圈内，要求△ABC和△DEF的每条边上三个圆圈内数字之和都等于18，则x+y+z的和是（　　）

  A．6

  B．15

  C．18

  D．24
  组卷：619引用：2难度：0.5

  解析

三.解答题（共5小题，满分48分）

• 16．某商场若购进2部甲型号手机和3部乙型号手机，共需7400元；若购进3部甲型号手机和5部乙型号手机，共需11700元．
  （1）求甲、乙型号手机每部的进价；
  （2）商场计划用不少于44400元且不多于50000元的资金购进这两种型号手机共30部．
  ①求有多少种进货方案；
  ②若每部甲，乙型号手机的售价分别为2500元，1950元，采用①中甲型手机进货量最少的方案进货，为了促销．商场决定每售出一部甲型号手机，返还顾客现金a元，每售出一部乙型号手机，返还顾客现金b元（a≥50，b≥50且a、b为50的整数倍），要保证该进货方案（全都售完）获利达到16500元，直接写出a、b的值．
  组卷：205引用：5难度：0.6

  解析

• 17．在平面直角坐标系中，点A在第一象限，AB⊥x轴于点B，AC⊥y轴于点C，已知点B（b,0），C（0，c），其中b,c满足|b-8|+

  c

  -

  6

  =0．
  
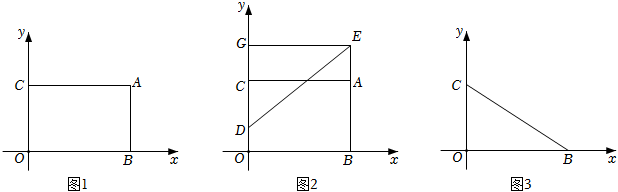
  （1）直接写出点A坐标．
  （2）如图2，点D从点O出发以每秒1个单位的速度沿y轴正方向运动，同时点E从点A出发，以每秒2个单位的速度沿射线BA运动，过点E作GE⊥y轴于点G，设运动时间为t秒，当S_{四边形AEGC}＜S_△DEG时，求t的取值范围．
  （3）如图3，将线段BC平移，使点B的对应点M恰好落在y轴负半轴上，点C的对应点为N，连接BN交y轴于点P，当OM=4OP时，求点M的坐标．
  组卷：392引用：2难度：0.3

  解析