旗下产品
充值服务
试卷征集
申请校本题库
智能组卷
错题库
五大核心功能
试卷征集
加入会员
操作视频

设
S
1
=
1
+
1
1
2
+
1
2
2
，
S
2
=
1
+
1
2
2
+
1
3
2
，
S
3
=
1
+
1
3
2
+
1
4
2
，…，
S
n
=
1
+
1
n
2
+
1
（
n
+
1
）
2
，则
S
1
+
S
2
+
…
+
S
14
的值为（　　）

【考点】分式的加减法；算术平方根．
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
当前模式为游客模式，立即登录查看试卷全部内容及下载
发布：2024/7/9 8:0:8组卷：242引用：1难度：0.5
相似题

  • 1．若记f（x）=
    x
    2
    1
    +
    x
    2
    ，例如f（1）=
    1
    2
    1
    +
    1
    2
    =
    1
    2
    ，f（
    1
    2
    ）=
    （
    1
    2
    ）
    2
    1
    +
    （
    1
    2
    ）
    2
    =
    1
    5
    ，则f（1）+f（2）+f（
    1
    2
    ）+f（3）+f（
    1
    3
    ）+…+f（2022）+f（
    1
    2022
    ）=
    ．

    发布：2025/6/13 22:30:1组卷：114引用：1难度：0.7
    解析

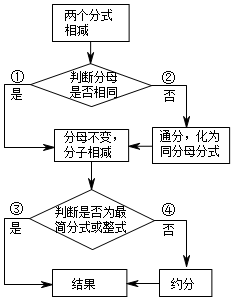  • 2．学习分式运算过程中，老师布置了这样一个任务：依据右侧的流程图，计算
    a
    a
    -
    b
    -
    2
    ab
    a
    2
    -
    b
    2
    ．
    （1）依据右侧流程图计算
    a
    a
    -
    b
    -
    2
    ab
    a
    2
    -
    b
    2
    时，需要经历的路径是
    （只填写序号）；
    （2）依据（1）中路径写出正确解答过程．

    发布：2025/6/13 22:30:1组卷：177引用：4难度：0.7
    解析

  • 3．计算
    m
    2
    m
    -
    1
    -
    2
    m
    -
    1
    m
    -
    1
    的结果是（　　）

    发布：2025/6/13 18:30:2组卷：2683引用：22难度：0.8
    解析
相关试卷
商务合作服务条款走进菁优
帮助中心兼职招聘意见反馈
深圳市菁优智慧教育股份有限公司
粤ICP备10006842号公网安备44030502001846号
©2010-2025 jyeoo.com 版权所有
深圳市市场监管
主体身份认证
APP开发者：深圳市菁优智慧教育股份有限公司| 应用名称：菁优网 | 应用版本：5.0.7 |隐私协议|第三方SDK|用户服务条款
广播电视节目制作经营许可证|出版物经营许可证|网站地图
本网部分资源来源于会员上传，除本网组织的资源外，版权归原作者所有，如有侵犯版权，请立刻和本网联系并提供证据，本网将在三个工作日内改正