2023-2024学年河北省衡水市武强中学高一(上)期末数学试卷
发布:2025/11/23 9:0:23
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知函数
在f(x)=sin(ωx-π6)(ω>0)上单调递减,则ω的取值范围是( )(π2,π)组卷:159引用:1难度:0.6 -
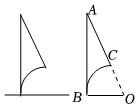 2.如图,某次帆船比赛LOGO的设计方案如下:在直角三角形ABO中挖去以点O为圆心,OB为半径的扇形BOC,使得扇形BOC的面积是直角三角形ABO面积的一半.记∠AOB=α,则的值为( )1-cos2α+sin2α2α•sinα•cosα组卷:13引用:1难度:0.7
2.如图,某次帆船比赛LOGO的设计方案如下:在直角三角形ABO中挖去以点O为圆心,OB为半径的扇形BOC,使得扇形BOC的面积是直角三角形ABO面积的一半.记∠AOB=α,则的值为( )1-cos2α+sin2α2α•sinα•cosα组卷:13引用:1难度:0.7 -
3.设f(x)是定义在R上的函数,对任意x,y∈R,恒有f(x+y)=f(x)•f(y),当x>0时,有0<f(x)<1.则下列说法正确的是( )
组卷:7引用:0难度:0.5 -
4.设
,则a,b,c的大小关系为( )a=log23,b=log45,c=2-0.1组卷:480引用:2难度:0.7 -
5.已知函数f(x)=ax5+bx3+cx+1(abc≠0),若f(-2)=5,则f(2)=( )
组卷:34引用:1难度:0.7 -
6.已知集合A={x|
>1},B={x|lgx<0},则A∪B=( )2x组卷:124引用:2难度:0.8 -
7.cos
=( )13π6组卷:891引用:10难度:0.8 -
8.y=(2k-1)x+b是R上的减函数,则有( )
组卷:1091引用:5难度:0.8
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9.下列选项正确的是( )
组卷:157引用:4难度:0.7 -
10.下列函数中,既是偶函数又在区间(0,+∞)上是增函数的是( )
组卷:70引用:8难度:0.7 -
11.若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象不可能是( )
组卷:81引用:1难度:0.8 -
12.已知函数f(x)=sinx+
cosx,则下列结论正确的是( )3组卷:477引用:6难度:0.8
三、填空题:本题共4小题,每小题5分,共20分.
-
13.函数y=sinx的定义域是[a,b],值域是[-1,
],则b-a的最大值与最小值之和是.-12组卷:294引用:5难度:0.9 -
14.已知函数f(x)=
,则f(f(-2))=;若f(x)≥2,则实数x的取值范围是 .2x,x≥0log2(-x),x<0组卷:76引用:3难度:0.7 -
15.已知幂函数
,若f(a-1)<f(8-2a),则a的取值范围是 .f(x)=(1x)110组卷:374引用:7难度:0.7 -
16.已知集合A={x|x2-6x+8≤0},B={x||x-3|<2,x∈Z},则A∩B=.
组卷:381引用:4难度:0.7
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17.已知函数y=ax2+(a+b)x-3.
(1)当a=-2时,不等式ax2+(a+b)x-3≤b对∀x∈(1,+∞)恒成立,求实数b的取值范围;
(2)当b=-3时,解关于x的不等式ax2+(a+b)x-3<0.组卷:192引用:3难度:0.7 -
18.已知幂函数y=f(x)的图象过点(8,m)和(9,3).
(1)求实数m的值;
(2)若函数g(x)=af(x)(a>0,a≠1)在区间[4,16]上的最大值等于最小值的2倍,求实数a的值.组卷:25引用:2难度:0.7 -
19.椭圆
x2a2=1(a>b>1)的焦距为2c,直线l过点(b,0)和(0,c)+y2b2
(1)若b=2,c=3,求此椭圆的准线方程;
(2)若点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和为sa,求椭圆的离心率e的取值范围.≥45组卷:23引用:1难度:0.3 -
20.求下列各式的值.
(1)sin105°;
(2)sin(-);5π12
(3)tan15°;
(4)tan.7π12组卷:9引用:1难度:0.7 -
21.已知函数
.f(x)=2cosxsin(x+π6)-12
(1)求f(x)的最小正周期;
(2)求f(x)的单调递减区间以及在区间上的最值.[-7π12,-π4]组卷:282引用:2难度:0.6 -
22.已知二次函数y=ax2+bx+c(a>b>c)的图像过点(1,0),一次函数y=ax+b.
(1)求证:两函数的图象交于不同两点A、B;
(2)求线段AB在x轴上射影长的取值范围.组卷:9引用:1难度:0.5


