2022-2023学年福建省宁德市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．

• 1．若复数z=i（2+i）（i为虚数单位），则z的虚部为（　　）

  A．-1

  B．-2i

  C．2

  D．2i
  组卷：58引用：5难度：0.8

  解析

• 2．在△ABC中，D为线段AB上一点，且

  AD

  =

  1

  3

  AB

  ，则

  CD

  =（　　）

  A． 1 3 AB + AC

  B． AB + 1 3 AC

  C． 1 3 AB - AC

  D． AB - 1 3 AC
  组卷：30引用：1难度：0.7

  解析

• 3．设A，B为两个互斥事件，且P（A）＞0，P（B）＞0，则下列各式一定正确的是（　　）

  A．P（AB）=P（A）P（B）	B．P（A∪B）=P（A）+P（B）
  C．P（AB）=P（A）+P（B）	D．P（A∪B）=P（A）P（B）
  组卷：97引用：3难度：0.8

  解析

• 4．两条异面直线与同一平面所成的角，不可能是（　　）

  A．两个角都是直角

  B．两个角都是锐角

  C．两个角都为0°

  D．一个角为0°，一个角为90°
  组卷：41引用：1难度：0.5

  解析

• 5．某学校高年级有300名男生，200名女生，现采用分层随机抽样的方法调查数学考试成绩，抽取一个容量为60的样本，男生平均成绩为110分，女生平均成绩为100分，那么可以推测高一年级学生的数学平均成绩约为（　　）

  A．100分

  B．105分

  C．106分

  D．110分
  组卷：53引用：1难度：0.8

  解析

• 6．设a,b是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（　　）

  A．若α∥β，a⊂α，b⊂β，则a∥b	B．若α∩β=a,b∥a,则b∥α
  C．若α⊥β，a⊂α，b⊂β，则a⊥b	D．若a⊥α，b⊂β，α∥β，则a⊥b
  组卷：61引用：4难度：0.7

  解析

• 7．位于某海域A处的甲船获悉，在其正东方向相距20nmile的B处有一艘渔船遇险后抛锚等待营救，甲船立即前往救援，同时把消息告知位于甲船南偏西30°，且与甲船相距10n mile的C处的乙船．乙船也立即朝着渔船前往营救，则sin∠ACB=（　　）

  A． 21 7

  B． 7 7

  C． 3 7

  D． 7 3
  组卷：53引用：2难度：0.6

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

• 21．已知锐角△ABC的内角A，B，C所对的边分别是a,b,c.请从条件①、条件②中选择一个条件作为已知，求：
  （1）A的度数：
  （2）若c=1，求△ABC面积的取值范围．
  条件①：

  acos

  C

  +

  3

  asin

  C

  =

  b

  +

  c

  ；
  条件②：△ABC的面积

  S

  =

  3

  （

  b

  2

  +

  c

  2

  -

  a

  2

  ）

  4

  ．
  组卷：30引用：2难度：0.6

  解析

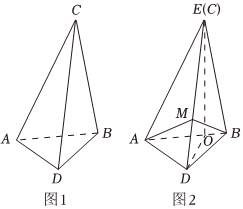• 22．如图1，平面四边形ACBD满足AB⊥CD，AB∩CD=O，AO=3，BO=1，

  CO

  =

  3

  3

  ，

  DO

  =

  3

  ．将三角形ABC沿着AB翻折到三角形ABE的位置，连接ED得到三棱锥E-ABD（如图2）．
  （1）证明：AB⊥DE；
  （2）若平面ABE⊥平面ABD，M是线段DE上的一个动点，记∠ABM，∠BAM分别为α，β，当α-β取得最大值时，求二面角M-AB-D的余弦值．
  组卷：33引用：1难度：0.4

  解析