2022-2023学年辽宁省鞍山市千山区九年级（上）期末数学试卷

一、选择题（每题3分，共24分）

• 1．-2的绝对值是（　　）

  A．2

  B．-2

  C． 1 2

  D．- 1 2
  组卷：6524引用：784难度：0.9

  解析

• 2．在下列函数中y随x增大而减小的函数是（　　）

  A．y=5x

  B． y = - 2 x

  C．y=-2x

  D．y=x2
  组卷：51引用：3难度：0.7

  解析

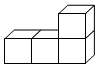• 3．如图，是由棱长都相等的四个小正方体组成的几何体．该几何体的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：32引用：3难度：0.8

  解析

• 4．下列说法正确的是（　　）

  A．“367人中必有2人的生日是同一天”是必然事件

  B．了解一批灯泡的使用寿命采用全面调查

  C．一组数据6，5，3，5，4的众数是5，中位数是3

  D．一组数据10，11，12，9，8的平均数是10，方差是1.5
  组卷：473引用：11难度：0.6

  解析

• 5．如图，正方形ABCD的两条对角线AC，BD相交于点O，点E在BD上，且BE=CD，则∠BEC的度数为（　　）

  A．22.5°

  B．60°

  C．67.5°

  D．75°
  组卷：719引用：11难度：0.7

  解析

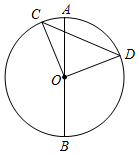• 6．如图，AB是⊙O的直径，CD是弦，点C，D在直径AB的两侧．若∠AOC：∠AOD：∠DOB=2：7：11，CD=4，则

  ˆ

  CD

  的长为（　　）

  A．2π

  B．4π

  C． 2 π 2

  D． 2 π
  组卷：2511引用：9难度：0.5

  解析

• 7．如图，在△ABC中，BF平分∠ABC，AF⊥BF于点F，D为AB的中点，连接DF延长交AC于点E．若AB=10，BC=16，则线段EF的长为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：6460引用：44难度：0.7

  解析

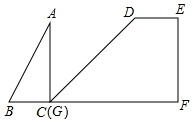• 8．如图，在四边形DEFG中，∠E=∠F=90°，∠DGF=45°，DE=1，FG=3，Rt△ABC的直角顶点C与点G重合，另一个顶点B（在点C左侧）在射线FG上，且BC=1，AC=2．将△ABC沿GF方向平移，点C与点F重合时停止．设CG的长为x,△ABC在平移过程中与四边形DEFG重叠部分的面积为y,则下列图象能正确反映y与x函数关系的是（　　）

  A．

  B．

  C．

  D．
  组卷：1173引用：6难度：0.6

  解析

三、解答题（共102分）

• 25．【证明体验】
  （1）如图1，AD为△ABC的角平分线，∠ADC=60°，点E在AB上，AE=AC．求证：DE平分∠ADB．
  【思考探究】
  （2）如图2，在（1）的条件下，F为AB上一点，连结FC交AD于点G．若FB=FC，DG=2，CD=3，求BD的长．
  【拓展延伸】
  （3）如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA=2∠DCA，点E在AC上，∠EDC=∠ABC．若BC=5，CD=2

  5

  ，AD=2AE，求AC的长．
  
  组卷：5874引用：24难度：0.3

  解析

• 26．如图1，抛物线y=-x²+bx+c与x轴交于点A和点B，与y轴交于点C，直线y=x+4经过点A和点C．
  （1）求抛物线的解析式；
  （2）如图2，点P为y轴左侧抛物线上一动点，连CP、CB和AP．
  ①当点P在直线AC上方时，连PB交AC于D，记M=S_△APC-S_△BPC，求M的最大值及M取最大值时点P的坐标？
  ②当点P满足∠CBA-∠PCA=45°时，直接写出P点坐标为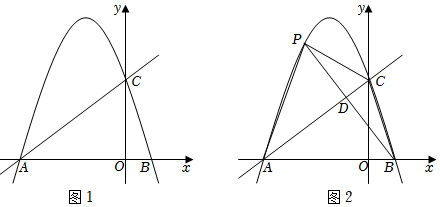

  ．
  
  组卷：916引用：3难度：0.2

  解析