2022-2023学年内蒙古赤峰二中高一（下）第二次月考数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．设i为虚数单位，复数z满足z（1-i）=2i,则|z|=（　　）

  A．1

  B． 2

  C．2

  D．2 2
  组卷：163引用：18难度：0.8

  解析

• 2．已知向量

  a

  =

  （

  -

  1

  ，

  x

  ）

  ，

  b

  =

  （

  2

  ，

  1

  ）

  ，若

  a

  ⊥

  b

  ，则x的值为（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：293引用：6难度：0.8

  解析

• 3．在△ABC中，角A、B、C对的边分别为a、b、c,若a=4，b=5，

  c

  =

  61

  ，则角C等于（　　）

  A．120°

  B．90°

  C．60°

  D．45°
  组卷：219引用：8难度：0.7

  解析

• 4．下列关于空间几何体结构特征的描述错误的是（　　）

  A．棱柱的侧棱互相平行

  B．以直角三角形的一边为轴旋转一周得到的几何体不一定是圆锥

  C．正三棱锥的各个面都是正三角形

  D．棱台各侧棱所在直线会交于一点
  组卷：167引用：4难度：0.9

  解析

• 5．若

  a

  =

  （

  3

  ，

  4

  ）

  ，

  b

  =

  （

  5

  ，

  12

  ）

  ，则

  a

  与

  b

  的夹角的余弦值为（　　）

  A． 63 65

  B． 33 65

  C． - 33 65

  D． - 63 65
  组卷：94引用：6难度：0.7

  解析

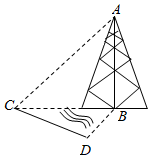• 6．如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个观测点C，D，测得∠BCD=15°，∠CBD=30°，CD=10

  2

  m,并在C处测得塔顶A的仰角为45°，则塔高AB=（　　）

  A．30 2 m

  B．20 3 m

  C．30m

  D．20m
  组卷：192引用：12难度：0.7

  解析

• 7．一个圆锥的底面圆和顶点都恰好在球O的球面上，且球心O在圆锥体内部，若球O的表面积为16π，O到圆锥底面圆的距离为1，则该圆锥的侧面积为（　　）

  A．6π

  B．4π

  C．3π

  D．2π
  组卷：130引用：2难度：0.7

  解析

四、解答题（本大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤）

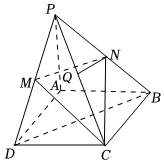• 21．如图，在四棱锥P-ABCD中，底面ABCD是菱形，N，M，Q分别为PB，PD，PC的中点．
  （1）求证：QN∥平面PAD；
  （2）记平面CMN与底面ABCD的交线为l,试判断直线l与平面PBD的位置关系，并证明．
  组卷：496引用：3难度：0.7

  解析

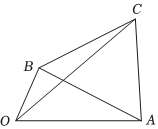• 22．如图，四边形OACB中，OA=2，OB=1，三角形ABC为正三角形．
  （1）当

  ∠

  AOB

  =

  π

  3

  时，设

  OC

  =

  x

  OA

  +

  y

  OB

  ，求x,y的值；
  （2）设∠AOB=θ（0＜θ＜π），则当θ为多少时．
  ①四边形OACB的面积S最大，最大值是多少？
  ②线段OC的长最大，最大值是多少？
  组卷：44引用：3难度：0.5

  解析