2023年湖北省襄阳市六校联考中考数学模拟试卷

一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)

• 1．在实数

  -

  2

  ，

  3

  ，

  0

  ，-π中，最小的数是（　　）

  A． 3

  B．0

  C．-π

  D．-2
  组卷：189引用：4难度：0.8

  解析

• 2．下列四个几何体中，左视图为圆的是（　　）

  A．

  B．

  C．

  D．
  组卷：2340引用：105难度：0.9

  解析

• 3．下列各式中，计算结果为m⁸的是（　　）

  A．m2•m4

  B．m4+m4

  C．m16÷m2

  D．（m2）4
  组卷：701引用：8难度：0.7

  解析

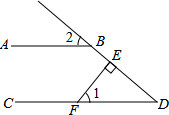• 4．如图，AB∥CD，FE⊥DB，垂足为E，∠1=60°，则∠2的度数是（　　）

  A．60°

  B．50°

  C．40°

  D．30°
  组卷：761引用：9难度：0.7

  解析

• 5．下列图形中，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：24引用：1难度：0.5

  解析

• 6．下列说法错误的是（　　）

  A．掷一枚硬币，正面朝上这一事件是随机事件

  B．天气预报说明天的降水概率是80%，则明天一定会下雨

  C．在单词mathematics（数学）中任意选择一个字母“a”的概率为 2 11

  D．任意画一个五边形，其内角和是540°这一事件是必然事件
  组卷：55引用：3难度：0.7

  解析

• 7．某中学组织初三学生篮球比赛，以班为单位，每两班之间都比赛一场，计划安排15场比赛，则共有多少个班级参赛？（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：3557引用：40难度：0.7

  解析

• 8．《九章算术》是中国传统数学的重要著作之一，奠定了中国传统数学的基本框架，其中记载的一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”其大意是：一根竹子原高1丈（1丈=10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？若设折断处离地面x尺，则下面所列方程正确的是（　　）

  A． 3 x + 1 = 1 10 - x	B． 1 3 （ 10 - x ） = 7 10
  C．x2+32=（10-x）2	D．x2+72=（10-x）2
  组卷：851引用：10难度：0.6

  解析

三、解答题(本大题共9小题,共73.0分。解答应写出文字说明,证明过程或演算步骤)

• 24．一次小组合作探究课上，老师将两个正方形按如图1所示的位置摆放（点E，A，D在同一条直线上）．
  （1）证明推断
  将正方形AEFG绕点A按逆时针方向旋转到如图2所示的位置．
  ①求证：BE=DG；②推断：BE与DG的位置关系为

  ；
  （2）类比探究
  将（1）中的正方形分别改写成矩形AEFG和矩形ABCD，将矩形AEFG绕点A按顺时针方向旋转（如图3），且

  AE

  AG

  =

  AB

  AD

  =

  a

  b

  ．探究BE与DG的数量关系（用含a,b的式子表示），并写出探究过程．
  （3）拓展运用
  如图4，在（2）的条件下，当

  AE

  AG

  =

  AB

  AD

  =

  2

  3

  ，AE=4，AB=8，连接DE，BG．小组发现：在旋转过程中，DE²+BG²的值是定值，请求出这个定值．
  
  组卷：215引用：2难度：0.3

  解析

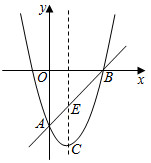• 25．如图，在平面直角坐标系中，已知抛物线y=ax²-2x+c与直线y=kx+b都经过
  A（0，-3）、B（3，0）两点，该抛物线的顶点为C．
  （1）求此抛物线和直线AB的解析式；
  （2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过点M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，试求出点M的坐标；若不存在，请说明理由；
     （3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，试求出点P的坐标，并求出△PAB面积的最大值．
  组卷：510引用：2难度：0.2

  解析