2022-2023学年湖北省潜江市园林高级中学高二（上）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分．在每个小题给出的选项中，只有一项是符合题目要求的．

• 1．已知

  a

  =

  （

  1

  ，

  1

  ，

  1

  ）

  为平面α的一个法向量，A（1，0，0）为α内的一点，则点D（1，1，2）到平面α的距离为（　　）

  A． 3

  B． 2

  C． 5 2

  D． 6 3
  组卷：233引用：11难度：0.7

  解析

• 2．已知椭圆

  x

  2

  3

  +

  y

  2

  4

  =

  1

  的上焦点为F，以F点为圆心，且与一条坐标轴相切的圆的方程为（　　）

  A．x2+y2-2y=0	B．x2+y2-2x=0
  C． x 2 + y 2 - 1 8 y = 0	D． x 2 + y 2 - 1 8 x = 0
  组卷：14引用：2难度：0.7

  解析

• 3．已知空间向量

  a

  ，

  b

  ，

  c

  满足

  a

  +

  b

  +

  c

  =

  0

  ，

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，

  |

  c

  |

  =

  7

  ，则

  a

  与

  b

  的夹角为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：457引用：14难度：0.6

  解析

• 4．若抛物线y²=4x的弦AB中点坐标为

  （

  1

  ，

  1

  2

  ）

  ，则直线AB的斜率为（　　）

  A．-4

  B．4

  C．-2

  D．2
  组卷：19引用：2难度：0.7

  解析

• 5．已知直三棱柱ABC-A₁B₁C₁中，∠ABC=120°，AB=2，BC=CC₁=1，则异面直线AB₁与BC₁所成角的余弦值为（　　）

  A． 3 2

  B． 15 5

  C． 10 5

  D． 3 3
  组卷：10030引用：67难度：0.6

  解析

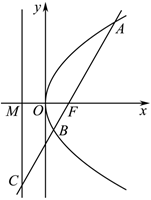• 6．如图，过抛物线y²=2px（p＞0）的焦点F的直线l交抛物线于点A，B，交其准线于点C，准线与对称轴交于点M，若

  |

  BC

  |

  |

  BF

  |

  =

  3

  ，且|AF|=3，则p为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：648引用：8难度：0.6

  解析

• 7．已知点A（-5，0），B（5，0），动点P（m,n）满足：直线PA的斜率与直线PB的斜率之积为

  -

  16

  25

  ，则4m²+n²的取值范围为（　　）

  A．[16，100]

  B．[25，100]

  C．[16，100）

  D．（25，100）
  组卷：240引用：7难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出相应的文字说明、证明过程或演算步骤．

• 21．已知抛物线的顶点为原点，焦点F在x轴的正半轴，F到直线x-y+2=0的距离为

  5

  2

  4

  ．点N（x₀，y₀）（y₀＞0）为此抛物线上的一点，

  |

  NF

  |

  =

  5

  2

  ．直线l与抛物线交于异于N的两点A，B两点，且k_NA•k_NB=-2．
  （1）求抛物线方程和N点坐标；
  （2）求证：直线AB过定点，并求该定点坐标．
  组卷：73引用：3难度：0.5

  解析

• 22．已知直线l过椭圆C₁：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦点F且与椭圆C₁交于A、B两点，直线l与双曲线C₂：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1的两条渐近线l₁、l₂分别交于M、N两点．
  （1）若|OF|=

  3

  ，且当l⊥x轴时，△MON的面积为

  3

  2

  ，求双曲线C₂的方程；
  （2）如图所示，若椭圆C₁的离心率e=

  2

  2

  ，l⊥l₁且

  FA

  =

  λ

  AN

  （λ＞0），求实数λ的值．
  组卷：31引用：1难度：0.6

  解析