2023-2024学年广东省肇庆中学大旺实验学校高二（上）开学数学试卷

一、单选题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。）

• 1．复数

  5

  2

  -

  i

  =（　　）

  A．2+i

  B．-2+i

  C．-2-i

  D．2-i
  组卷：112引用：5难度：0.8

  解析

• 2．甲、乙同时参加某次法语考试，甲、乙考试达到优秀的概率分别为0.6，0.7，两人考试相互独立，则甲、乙两人都未达到优秀的概率为（　　）

  A．0.42

  B．0.28

  C．0.18

  D．0.12
  组卷：219引用：5难度：0.8

  解析

• 3．若一组样本数据x₁，x₂，…，x_n的方差为0.01，则数据4x₁+1，4x₂+1，4x₃+1，…，4x_n+1的方差为（　　）

  A．0.04

  B．0.16

  C．1.04

  D．1.16
  组卷：185引用：2难度：0.8

  解析

• 4．在△ABC中，角A，B，C的对边分别是a,b,c,若

  a

  =

  3

  ，

  c

  =

  8

  ，

  B

  =

  π

  3

  ，则b=（　　）

  A．6

  B．7

  C． 61

  D． 95
  组卷：189引用：4难度：0.7

  解析

• 5．已知点A（1，-1，2）关于y轴的对称点为B，则|AB|=（　　）

  A． 2 5

  B． 2 6

  C．2

  D． 3 2
  组卷：159引用：2难度：0.7

  解析

• 6．P是△ABC所在平面内一点，若

  CB

  =λ

  PA

  +

  PB

  ，其中λ∈R，则P点一定在（　　）

  A．△ABC内部	B．AC边所在直线上
  C．AB边所在直线上	D．BC边所在直线上
  组卷：916引用：26难度：0.7

  解析

• 7．已知向量

  a

  =（k,3），

  b

  =（1，4），

  c

  =（2，1）且（2

  a

  -3

  b

  ）⊥

  c

  ，则实数k=（　　）

  A．- 9 2

  B．0

  C．3

  D． 15 2
  组卷：4260引用：74难度：0.9

  解析

四、解答题（本大题共6大题，共70分，解答应写出文字说明、证明过程或演算步骤．）

• 21．记钝角△ABC的内角A，B，C的对边分别为a,b,c,已知

  cos

  A

  1

  -

  sin

  A

  =

  cos

  A

  +

  cos

  B

  1

  -

  sin

  A

  +

  sin

  B

  ．
  （1）若

  C

  =

  2

  π

  3

  ，求A；
  （2）求

  a

  2

  +

  c

  2

  b

  2

  的取值范围．
  组卷：115引用：3难度：0.5

  解析

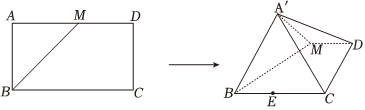• 22．如图，在矩形ABCD中，AB=1，

  BC

  =

  3

  ，M是线段AD上的一动点，将△ABM沿着BM折起，使点A到达点A'的位置，满足点A'∉平面BCDM且点A'在平面BCDM内的射影E落在线段BC上．
  （1）当点M与端点D重合时，证明：A'B⊥平面A'CD；
  （2）求三棱锥E-A'BM的体积的最大值；
  （3）设直线CD与平面A'BM所成的角为α，二面角A'-BM-C的平面角为β，求2sinα•cosβ的最大值．
  组卷：25引用：1难度：0.4

  解析