2023-2024学年天津市滨海新区泰达一中高二（上）期中数学试卷

一、单选题（本大题共10小题，共40分）

• 1．已知直线倾斜角为60°，在y轴上的截距为-2，则此直线方程为（　　）

  A．y= 3 x+2

  B．y=- 3 x+2

  C．y=- 3 x-2

  D．y= 3 x-2
  组卷：723引用：16难度：0.9

  解析

• 2．与直线3x+4y+5=0关于y轴对称的直线方程为（　　）

  A．3x+4y-5=0

  B．3x+4y+5=0

  C．3x-4y+5=0

  D．3x-4y-5=0
  组卷：246引用：5难度：0.6

  解析

• 3．已知圆M：x²+（y-2）²=4，圆N：（x-1）²+（y-1）²=1，则圆M与圆N的位置关系是（　　）

  A．内切

  B．相交

  C．外切

  D．外离
  组卷：91引用：2难度：0.7

  解析

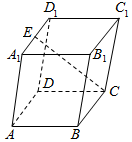• 4．如图，在平行六面体ABCD-A₁B₁C₁D₁中，E为A₁D₁的中点，设

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则

  CE

  =（　　）

  A． - a - 1 2 b + c

  B． a - 1 2 b + c

  C． a - 1 2 b - c

  D． a + 1 2 b - c
  组卷：1304引用：13难度：0.7

  解析

• 5．如果直线l₁：x+2ay-1=0与直线l₂：（3a-1）x-ay-1=0平行，则a=（　　）

  A．0

  B． 1 6

  C．0或1

  D．0或 1 6
  组卷：360引用：17难度：0.9

  解析

• 6．已知空间向量

  a

  =

  （

  2

  ，-

  1

  ，

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  2

  ，

  1

  ）

  ，则向量

  b

  在向量

  a

  上的投影向量是（　　）

  A． （ 4 3 ，- 2 3 ， 4 3 ）	B．（2，-1，2）
  C． （ 2 3 ，- 4 3 ， 2 3 ）	D．（1，-2，1）
  组卷：1495引用：16难度：0.6

  解析

三、解答题（本大题共4小题，共50分）

• 19．已知圆C：（x-a）²+（y-2）²=4（a＞0）及直线l：x-y+3=0．直线l被圆C截得的弦长为

  2

  2

  ．
  （1）求a的值；
  （2）求过点（3，5）并与圆C相切的切线方程．
  组卷：861引用：12难度：0.3

  解析

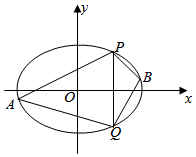• 20．已知椭圆C的中心在原点，焦点在x轴上，离心率为

  1

  2

  ，短轴长为4

  3

  ．
  （1）求椭圆C的标准方程；
  （2）直线x=2与椭圆C交于P，Q两点，A，B是椭圆C上位于直线PQ两侧的动点，且直线AB的斜率为

  1

  2

  ．
  （i）求四边形APBQ面积的最大值；
  （ii）设直线PA的斜率为k₁，直线PB的斜率为k₂，判断k₁+k₂的值是否为常数，并说明理由．
  组卷：1704引用：15难度：0.1

  解析