2022-2023学年湖北省武汉市华中科大附中高二（上）月考数学试卷（9月份）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．若复数z满足z（1-i）=i,则下列说法正确的是（　　）

  A．z的虚部为 1 2 i

  B．z的共轭复数为 z = - 1 2 + 1 2 i

  C．z对应的点在第二象限

  D．|z|=1
  组卷：42引用：2难度：0.8

  解析

• 2．在下列条件中，一定能使空间中的四点M，A，B，C共面的是（　　）

  A． OM = 2 OA - OB - OC	B． OM = 1 5 OA + 1 3 OB + 1 2 OC
  C． MA + 2 MB + MC = 0	D． OM + OA + OB + OC = 0
  组卷：516引用：11难度：0.7

  解析

• 3．已知向量

  n

  =（2，0，1）为平面α的法向量，点A（-1，2，1）在α内，则P（1，2，2）到α的距离为（　　）

  A． 5 5

  B． 5

  C．2 5

  D． 5 10
  组卷：183引用：14难度：0.9

  解析

• 4．已知A，B，C，D，E是空间中的五个点，其中点A，B，C不共线，则“存在实数x,y,使得

  DE

  =x

  AB

  +y

  AC

  是“DE∥平面ABC”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：343引用：10难度：0.8

  解析

• 5．在△ABC中，角A，B，C的对边分别为a,b,c,且c-2bsinC=0，B∈（0，

  π

  2

  ），b=1，a=

  3

  ，则△ABC的面积为（　　）

  A． 3 4 或 1 4

  B． 3 2 或 1 4

  C． 3 4 或 3 2

  D． 3 4 或 3 4
  组卷：118引用：4难度：0.7

  解析

• 6．为庆祝中国共产党成立100周年，甲、乙、丙三个小组进行党史知识竞赛，每个小组各派5位同学参赛，若该组所有同学的得分都不低于7分，则称该组为“优秀小组”（满分为10分且得分都是整数），以下为三个小组的成绩数据，据此判断，一定是“优秀小组”的是（　　）
  甲：中位数为8，众数为7；
  乙：中位数为8，平均数为8.4；
  丙：平均数为8，方差小于2．

  A．甲

  B．乙

  C．丙

  D．无法确定
  组卷：200引用：4难度：0.9

  解析

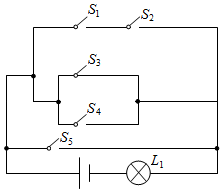• 7．如图，已知电路中有5个开关，开关S₅闭合的概率为

  1

  3

  ，其它开关闭合的概率都是

  1

  2

  ，且是相互独立的，则灯亮的概率为（　　）

  A． 7 8

  B． 15 16

  C． 23 24

  D． 4 5
  组卷：349引用：8难度：0.8

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步棸．

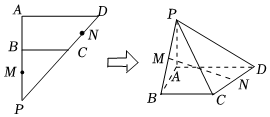• 21．如图，在等腰直角三角形PAD中，∠A=90°，AD=8，AB=3，B，C分别是PA，PD上的点，且AD∥BC，M，N分别为BP，CD的中点，现将△BCP沿BC折起，得到四棱锥P-ABCD，连结MN．
  （1）证明：MN∥平面PAD；
  （2）在翻折的过程中，当PA=4时，求平面PBC与平面PCD夹角的余弦值．
  组卷：117引用：5难度：0.5

  解析

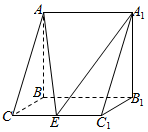• 22．如图，三棱柱ABC-A₁B₁C₁中，AB⊥侧面BB₁C₁C，已知∠BCC₁=

  π

  3

  ，BC=1，AB=C₁C=2，点E是棱C₁C的中点．
  （1）求证：C₁B⊥平面ABC；
  （2）在棱CA上是否存在一点M，使得EM与平面A₁B₁E所成角的正弦值为

  2

  11

  11

  ，若存在，求出

  CM

  CA

  的值；若不存在，请说明理由．
  组卷：223引用：7难度：0.4

  解析