当前位置：试卷中心 > 试卷详情

2023年四川省攀枝花市东区中考数学二模试卷

发布：2024/5/8 8:0:8

一、选择题：本大题共12个小题，每小题5分，共60分。每小题4个选项，其中只有一个选项是符合要求的。

1．下列整式与x²y为同类项的是（　　）
A．3xy B．2x²y C．x²yz D．-5xy²
组卷：479引用：4难度：0.9
解析
2．下列图形中，是中心对称图形的是（　　）
A． B． C． D．
组卷：155引用：10难度：0.9
解析
3．下列计算中，正确的是（　　）
A．（a-b）（-a-b）=a²-b² B．-2a（a-1）=-2a²-2a
C．
-
2
a
2
bc
÷
1
2
ab
=
-
4
ac
D．（-3a²b）²=6a⁴b²
组卷：23引用：1难度：0.6
解析
4．每年的4月7日是世界健康日，强调健康对于劳动创造和幸福生活的重要性，而血糖值（单位：mmol/L）对于治疗疾病和观察疾病都有指导意义．某人在每天的早晨空腹自测血糖值，并将一周的数据绘制成如图所示的折线统计图，则这组数据的中位数和众数分别是（　　）
A．4.3mmol/L，4.3mmol/L B．4.7mmol/L，4.0mmol/L
C．4.5mmol/L，4.3mmol/L D．4.7mmol/L，4.3mmol/L
组卷：178引用：3难度：0.7
解析
5．如图，在△ABC中，分别以A，C为圆心，大于
1
2
AC长为半径作弧，两弧分别相交于M，N两点，作直线MN，分别交线段BC，AC于点D，E，若AB=3，△ABD的周长为11，则BC的长度为（　　）
A．7 B．8 C．9 D．10
组卷：124引用：2难度：0.6
解析
6．下列二次根式中，不能与
3
合并的是（　　）
A．
32
B．
-
27
C．
12
D．
1
3
组卷：185引用：2难度：0.8
解析
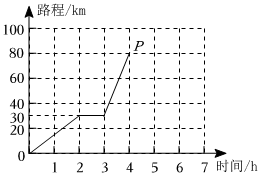7．骑自行车是一种健康自然的运动旅游方式，长期坚持骑自行车可增强心血管功能，提高人体新陈代谢和免疫力．如图是骑行爱好者老刘2023年2月12日骑自行车行驶路程（km）与时间（h）的关系图象，观察图象得到下列信息，其中错误的是（　　）
A．点P表示出发4h,老刘共骑行80km
B．老刘的骑行在0～2h的速度比3～4h的速度慢
C．0～2h老刘的骑行速度为15km/h
D．老刘实际骑行时间为4h
组卷：584引用：7难度：0.8
解析
8．用四根长度相等的木条制作学具，先制作图（1）所示的正方形ABCD，测得BD=10cm,活动学具成图（2）所示的四边形ABCD，测得∠A=120°，则图（2）中BD的长是（　　）
A．
5
3
cm B．
10
3
cm C．
5
6
cm D．
10
6
cm
组卷：219引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：本大题共8个小题，共70分.解答题应写出文字说明、证明过程或演算步骤

23．问题提出：已知矩形ABCD，点E为AB上的一点，EF⊥AB，交BD于点F．将△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E′BF′，则AE′与DF′有怎样的数量关系．

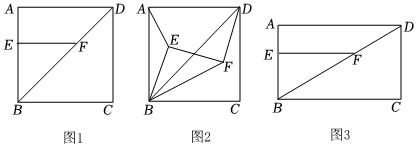
【问题探究】
探究一：如图，已知正方形ABCD，点E为AB上的一点，EF⊥AB，交BD于点F．
（1）如图1，直接写出
DF
AE
的值
；
（2）将△EBF绕点B顺时针旋转到如图2所示的位置，连接AE、DF，猜想DF与AE的数量关系，并证明你的结论；
探究二：如图，已知矩形ABCD，点E为AB上的一点，EF⊥AB，交BD于点F．
如图3，若四边形ABCD为矩形，
AB
BC
=
2
2
，将△EBF绕点B顺时针旋转α（0^o＜α≤90^o）得到△E′BF′（E、F的对应点分别为E′、F′点），连接AE′、DF′，则
AE
′
DF
′
的值是否随着α的变化而变化．若变化，请说明变化情况；若不变，请求出
AE
′
DF
′
的值．
【一般规律】
如图3，若四边形ABCD为矩形，BC=mAB，其它条件都不变，将△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E′BF′，连接AE′，DF′，请直接写出AE′与DF′的数量关系．
组卷：1009引用：3难度：0.3
解析
24．如图，已知抛物线y=ax²+bx+3的图象与x轴交于点A（1，0），B（-3，0），与y轴的正半轴交于点C．

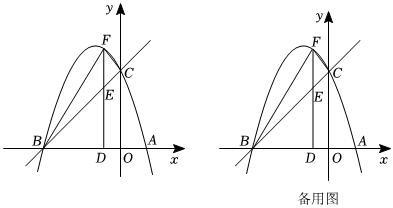
（1）求该抛物线的解析式；
（2）点D是线段OB上一动点，过点D作y轴的平行线，与BC交于点E，与抛物线交于点F．
①连接CF、BF，当△FBC的面积最大时，求此时点F的坐标；
②探究是否存在点D使得△CEF为直角三角形？若存在，求出点F的坐标；若不存在，说明理由．
组卷：998引用：9难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．（a-b）（-a-b）=a²-b²	B．-2a（a-1）=-2a²-2a
C． - 2 a 2 bc ÷ 1 2 ab = - 4 ac	D．（-3a²b）²=6a⁴b²

A．4.3mmol/L，4.3mmol/L	B．4.7mmol/L，4.0mmol/L
C．4.5mmol/L，4.3mmol/L	D．4.7mmol/L，4.3mmol/L

2023年四川省攀枝花市东区中考数学二模试卷

一、选择题：本大题共12个小题，每小题5分，共60分。每小题4个选项，其中只有一个选项是符合要求的。

1．下列整式与x2y为同类项的是（ ）

2．下列图形中，是中心对称图形的是（ ）

3．下列计算中，正确的是（ ）

5．如图，在△ABC中，分别以A，C为圆心，大于12AC长为半径作弧，两弧分别相交于M，N两点，作直线MN，分别交线段BC，AC于点D，E，若AB=3，△ABD的周长为11，则BC的长度为（ ）

6．下列二次根式中，不能与3合并的是（ ）

8．用四根长度相等的木条制作学具，先制作图（1）所示的正方形ABCD，测得BD=10cm,活动学具成图（2）所示的四边形ABCD，测得∠A=120°，则图（2）中BD的长是（ ）

三、解答题：本大题共8个小题，共70分.解答题应写出文字说明、证明过程或演算步骤

1．下列整式与x²y为同类项的是（　　）

2．下列图形中，是中心对称图形的是（　　）

3．下列计算中，正确的是（　　）

5．如图，在△ABC中，分别以A，C为圆心，大于
1
2
AC长为半径作弧，两弧分别相交于M，N两点，作直线MN，分别交线段BC，AC于点D，E，若AB=3，△ABD的周长为11，则BC的长度为（　　）

6．下列二次根式中，不能与
3
合并的是（　　）

8．用四根长度相等的木条制作学具，先制作图（1）所示的正方形ABCD，测得BD=10cm,活动学具成图（2）所示的四边形ABCD，测得∠A=120°，则图（2）中BD的长是（　　）