2022-2023学年辽宁省葫芦岛市高一(下)期末数学试卷
发布:2024/6/21 8:0:10
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1.
的值为( )sin17π4组卷:560引用:4难度:0.8 -
2.在复平面内,复数z=(1+i)(2-i)对应的点位于( )
组卷:278引用:12难度:0.9 -
3.在△ABC中,若acosA=bcosB,则△ABC的形状是( )
组卷:554引用:90难度:0.7 -
4.已知平面向量
=(-2,4),a=(1,2),若向量λb+a与b垂直,则实数λ的值为( )b组卷:73引用:2难度:0.8 -
5.欧拉公式eix=cosx+isinx是由瑞士著名数学家欧拉创立,该公式将指数函数的定义域扩大到复数,建立了三角函数与指数函数的关联,在复变函数论里面占有非常重要的地位,依据欧拉公式,下列选项正确的是( )
组卷:27引用:3难度:0.7 -
6.已知角α的终边经过点
,则(-1,3)=( )tan(-π+α)+cos(α-π2)组卷:495引用:2难度:0.7 -
7.《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥,若某直角圆锥内接于一球(圆锥的顶点和底面上各点均在该球面上),且该圆锥的侧面积为
,则此球的表面积为( )2π组卷:79引用:3难度:0.7
四、解答题(本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
-
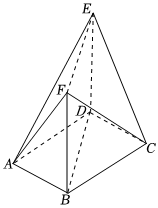 21.如图,在多面体ABCDEF中,菱形ABCD的边长为2,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3.
21.如图,在多面体ABCDEF中,菱形ABCD的边长为2,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3.
(1)在线段FC上确定一点H,使得平面BDH∥平面AEF;
(2)设G是线段EC的中点,在(1)的条件下,求二面角A—HG—B的大小.组卷:54引用:1难度:0.5 -
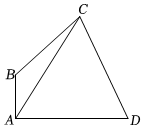 22.在△ABC中,角A,B,C的对边分别为a,b,c.已知AB⊥AD,,∠ACD=π3,AD=3
22.在△ABC中,角A,B,C的对边分别为a,b,c.已知AB⊥AD,,∠ACD=π3,AD=3
S△ABC=-32•BA.函数f(x)=BC(asinx+bsin2x)+acosx-bcos2x.3
(1)若a=b=1,求f(x)的值域;
(2)若对于任何有意义的边a,f(x)-1≥0在上有解,求b的取值范围.x∈(-π6,π3]组卷:45引用:4难度:0.5


