当前位置：试卷中心 > 试卷详情

2023-2024学年北京市海淀区首都师大附中七年级（上）月考数学试卷（10月份）

发布：2024/9/7 11:0:11

一、选择题（共10小题，每小题3分，共30分）

1．7的相反数是（　　）
A．
1
7
B．
-
1
7
C．7 D．-7
组卷：550引用：24难度：0.8
解析
2．据报道，2023年“五一”假期全国国内旅游出游合计274000000人次．数字274000000用科学记数法表示是（　　）
A．27.4×10⁷ B．2.74×10⁸ C．0.274×10⁹ D．2.74×10⁹
组卷：1441引用：26难度：0.9
解析
3．下列各式中，计算结果为1的是（　　）
A．-（-1） B．-|-1| C．（-1）³ D．-1⁴
组卷：816引用：18难度：0.8
解析
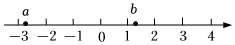4．有理数a,b在数轴上的对应点的位置如图所示，下列结论中正确的是（　　）
A．a＞-2 B．ab＞0 C．-a＜b D．|a|＞|b|
组卷：4538引用：48难度：0.7
解析
5．如图所示的程序计算，若开始输入的值为
-
1
2
，则输出的结果y是（　　）
A．25 B．30 C．45 D．40
组卷：2247引用：24难度：0.6
解析
6．若|m|=5，|n|=2，且m、n异号，则|m-n|的值为（　　）
A．7 B．3或-3 C．3 D．7或3
组卷：6002引用：55难度：0.7
解析
7．定义一种新运算：a*b=a²-3b,如2*1=2²-3×1=1，则（3*2）*（-1）的结果为（　　）
A．6 B．12 C．-12 D．-6
组卷：1047引用：8难度：0.7
解析
8．有理数m,n,k在数轴上的对应点的位置如图所示，若m+n＜0，n+k＞0，则A，B，C，D四个点中可能是原点的是（　　）
A．A点 B．B点 C．C点 D．D点
组卷：1154引用：30难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（第21题16分，第22、23题每题4分，第24题5分，第25题6分，

25．先阅读下面材料，再完成任务：
【材料】
下列等式：4-
3
5
=
4
×
3
5
+1，7-
3
4
=
7
×
3
4
+1，…，具有a-b=ab+1的结构特征，我们把满足这一特征的一对有理数称为“共生有理数对”，记作（a,b）．例如：
（
4
，
3
5
）
、
（
7
，
3
4
）
都是“共生有理数对”．
【任务】
（1）在两个数对（-2，1）、
（
2
，
1
3
）
中，“共生有理数对”是
．
（2）请再写出一对“共生有理数对”
；（要求：不与题目中已有的“共生有理数对”重复）
（3）若（x,-2）是“共生有理数对”，求x的值；
（4）若（m,n）是“共生有理数对”，判断（-n,-m）是不是“共生有理数对”，并说明理由．
组卷：1221引用：6难度：0.5
解析
26．在数轴上有A，B两点，点B表示的数为b.对点A给出如下定义：当b≥0时，将点A向右移动2个单位长度，得到点P；当b＜0时，将点A向左移动|b|个单位长度，得到点P．称点P为点A关于点B的“联动点”．如图，点A表示的数为-1．
（1）在图中画出当b=4时，点A关于点B的“联动点”P；
（2）点A从数轴上表示-1的位置出发，以每秒1个单位的速度向右运动．点B从数轴上表示7的位置同时出发，以相同的速度向左运动，两个点运动的时间为t秒．
①点B表示的数为
（用含t的式子表示）；
②是否存在t,使得此时点A关于点B的“联动点”P恰好与原点重合？若存在，请求出t的值；若不存在，请说明理由．
组卷：766引用：4难度：0.6
解析