2022-2023学年山东省济宁市邹城市七年级（下）期中数学试卷

一、选择题（本大题共10个小题，每小题3分，共30分．）

• 1．已知a＞0，b＜0，那么点P（a,b）在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：474引用：29难度：0.9

  解析

• 2．如图，下列条件不能判定直线a∥b的是（　　）

  A．∠1=∠2

  B．∠1=∠3

  C．∠1+∠4=180°

  D．∠2+∠4=180°
  组卷：566引用：39难度：0.9

  解析

• 3．三个实数-

  6

  ，-2，-

  7

  之间的大小关系是（　　）

  A．- 7 ＞- 6 ＞-2

  B．- 7 ＞-2＞- 6

  C．-2＞- 6 ＞- 7

  D．- 6 ＜-2＜- 7
  组卷：811引用：19难度：0.9

  解析

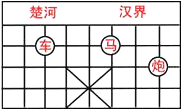• 4．如图，已知棋子“车”的坐标为（-2，3），棋子“马”的坐标为（1，3），则棋子“炮”的坐标为（　　）

  A．（3，2）

  B．（3，1）

  C．（2，2）

  D．（-2，2）
  组卷：1509引用：118难度：0.9

  解析

• 5．如图，已知a∥b,∠1=130°，则∠2等于（　　）

  A．30°

  B．50°

  C．70°

  D．130°
  组卷：50引用：2难度：0.5

  解析

• 6．点M（x,y）先向上平移2个单位，又向左平移3个单位得到点N的坐标为（0，0），则点M的坐标为（　　）

  A．（2，-3）

  B．（3，-2）

  C．（-2，3）

  D．（-3，2）
  组卷：155引用：4难度：0.7

  解析

• 7．若2m-4与3m-1是同一个数的平方根，则m的值是（　　）

  A．-3

  B．-1

  C．1

  D．-3或1
  组卷：11837引用：46难度：0.7

  解析

• 8．若a²=9，b³=-8，且ab＞0，则a-b的值为（　　）

  A．-1

  B．1

  C．5

  D．-1或5
  组卷：570引用：4难度：0.9

  解析

三、解答题（本大题共6个小题，共46分）

• 23．已知x-1的平方根是±2，4x+y的立方根是3，y-x的算术平方根是m.
  （1）求m的值；
  （2）如果5+m=a+b,其中a是整数，且0＜b＜1，求

  a

  -

  （

  2

  -

  b

  ）

  2

  ．
  组卷：412引用：4难度：0.7

  解析

• 24．阅读与理解：
  如图1，直线a∥b,点P在a,b之间，M，N分别为a,b上的点，P，M，N三点不在同一直线上，PM与a的夹角为α，PN与b的夹角为β，则∠MPN=α+β．
  理由如下：
  过P点作直线c∥b,因为a∥b,所以a∥c（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．所以∠1=α，∠2=β（两直线平行，内错角相等），所以∠1+∠2=α+β，即∠MPN=α+β．
  
  计算与说明：
  已知：平面上一点O和线段AB，CD，AB∥CD．
  （1）当点O在线段AB，CD之间时，如图2，AE平分∠OAB，CE平分∠OCD，若∠OAB=50°，∠OCD=60°，则∠E的度数为

  ．
  （2）当点O位于图3的位置时，连接OA，OC，请问：∠AOC与∠A，∠C有怎样的数量关系？并说明理由．
  组卷：227引用：2难度：0.6

  解析