当前位置：试卷中心 > 试卷详情

2020-2021学年安徽省池州市高三（上）期末数学试卷（理科）

发布：2025/11/17 11:0:34

一、选择题：共12小题，每小题5分，满分60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．i为虚数单位，复数
1
+
i
1
-
2
i
在复平面内对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：48引用：2难度：0.8
2．已知函数
f
（
x
）
=
2
cos
（
π
4
-
3
x
）
，
x
∈
[
-
π
2
，
π
2
]
，则f（x）的单调递增区间是（　　）
A．
[
-
π
2
，
0
]
B．
[
-
π
4
，
π
12
]
C．
[
-
π
2
，-
π
4
）
，
[
π
12
，
5
π
12
]
D．
[
-
π
4
，
π
12
]
，
[
5
π
12
，
π
2
]
组卷：358引用：10难度：0.7
3．已知向量
a
，
b
，
c
满足
|
a
|
=
|
b
|
=
2
，
|
c
|
=
2
3
，且
a
+
b
+
c
=
0
，则
cos
〈
a
，
b
〉
=（　　）
A．0 B．
3
2
C．
-
1
2
D．
1
2
组卷：55引用：1难度：0.7
4．抛物线C：y²=2px（p＞0）的焦点为F，且抛物线C与椭圆
x
2
2
+
y
2
=
1
在第一象限的交点为A，若AF⊥x轴，则p=（　　）
A．2 B．1 C．
2
2
3
D．
2
3
组卷：307引用：6难度：0.7
5．已知集合A={x|x²+2x-15＜0}，B={x|x＞1}，则A∪B等于（　　）
A．{x|x＞-5} B．{x|1＜x＜2} C．{x|x＞1} D．{x|x＜2}
组卷：20引用：1难度：0.9
6．设a=2^0.1，b=log₂0.1，c=cos0.1，则（　　）
A．a＞b＞c B．b＞a＞c C．c＞a＞b D．a＞c＞b
组卷：54引用：1难度：0.7
7．已知
sin
（
α
+
π
3
）
=
1
3
，则
cos
（
2
α
-
π
3
）
=（　　）
A．-
7
9
B．
7
9
C．-
2
9
D．
2
9
组卷：459引用：6难度：0.8

8．某品牌为了研究旗下某产品在淘宝、抖音两个平台的销售状况，统计了2021年7月到12月淘宝和抖音官方平台的月营业额（单位：万元），得到如图所示的折线图．下列说法错误的是（　　）

A．抖音平台的月营业额的平均值在[31，32]内

B．淘宝平台的月营业额总体呈上升趋势

C．抖音平台的月营业额极差比淘宝平台的月营业额极差小

D．10、11、12月份的总营业额淘宝平台比抖音平台少

组卷：141引用：1难度：0.8

9．执行如图所示的程序框图，输出的结果为（　　）
A．64 B．32 C．16 D．5
组卷：71引用：3难度：0.9
10．已知a=0.5²，b=2^0.5，c=log_0.52，则a,b,c的大小关系为（　　）
A．c＜b＜a B．a＜c＜b C．c＜a＜b D．b＜c＜a
组卷：119引用：4难度：0.9
11．已知双曲线C：x²-
y
2
24
=1的两焦点分别是F₁，F₂，双曲线C₁在第一象限部分有一点P，满足|PF₁|+|PF₂|=14．若圆C₂与△PF₁F₂三边都相切，则圆C₂的标准方程为（　　）
A．（x-1）²+（y-2）²=4 B．（x-1）²+（y-3）²=9
C．（x-2）²+（y-2）²=4 D．（x-2）²+（y-3）²=9
组卷：106引用：4难度：0.5
12．系统找不到该试题

二、填空题：共4小题每小题5分，满分20分。

13．已知点A（1，0），若点B是曲线y=f（x）上的点，且线段AB的中点在曲线y=g（x）上，则称点B是曲线y=f（x）关于曲线y=g（x）的一个“关联点“，已知f（x）=|log₂x|，g（x）=
（
1
2
）
x
，则曲线y=f（x）关于曲线y=g（x）的“关联点”的个数是
．
组卷：2引用：1难度：0.5
14．《易经》中记载着一种几何图形--八封图，图中正八边形代表八卦，中间的圆代表阴阳太极图，图中八块面积相等的曲边梯形代表八卦田．某中学开展劳动实习，去测量当地八卦田的面积如图，现测得正八边形的过长为8m,代表阴阳太极图的圆的半径为2m,则每块八卦田的面积为
m²．
组卷：94引用：4难度：0.6
15．若实数x,y满足：
x
-
y
≤
2
x
+
y
≥
2
x
+
3
y
≤
6
，则目标函数z=2x-y的最大值是
．
组卷：0引用：1难度：0.7
16．若某正方体的外接球的表面积为12π，则这个正方体内切球的半径为
．
组卷：214引用：1难度：0.8

三、解答题：满分60分。解答应写出文字说明，证明过程或演算步骤。第17-21题为必考题，每个试题考生都必须作答。第22、23题为选考题考生根据要求作答。（一）必考题：满分60分。

17．以直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系，且在两种坐标系中取相同的长度单位．曲线C的极坐标方程是ρ²=
16
1
+
3
co
s
2
θ
．
（Ⅰ）求曲线C的直角坐标方程；
（Ⅱ）设曲线C与x轴正半轴及y轴正半轴交于点M，N，在第一象限内曲线C上任取一点P，求四边形OMPN面积的最大值．
组卷：155引用：4难度：0.5
18．已知f（x）=|x+2|+|x-a|．
（1）当a=1时，求不等式f（x）≥5的解集；
（2）若f（x）＞2a恒成立，求实数a的取值范围．
组卷：6引用：1难度：0.5
19．设函数f（x）=x³-3ax+b（a≠0）在点（2，f（2））处与直线y=8相切．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间与极值．
组卷：21引用：5难度：0.5
20．在公差不为零的等差数列{a_n}和等比数列{b_n}中，已知a₁=1且a₁=b₁，a₂=b₂，a₅=b₃
（1）求等差数列{a_n}，等比数列{b_n}的通项公式
（2）当T_n=
1
a
n
a
a
+
1
，求数列{T_n}的前n项和．
组卷：17引用：2难度：0.3
21．甲、乙、丙三人参加浙江卫视的“我爱记歌词”节目，三人独立闯关，互不影响．其中甲过关而乙不过关的概率是
1
4
，乙过关而丙不过关的概率是
1
12
，甲、丙均过关的概率为
2
9
．记ξ为节目完毕后过关人数和未过关人数之差的绝对值．
（1）求甲、乙、丙三人各自过关的概率；
（2）理科：求ξ的分布列和数学期望；
文科：求ξ取最小值时的概率；
（3）理科：设“函数
f
（
x
）
=
lo
g
2
[
ξ
x
2
-
（
ξ
-
1
）
x
+
1
4
]
的值域是R”为事件D，试求事件D的概率．
文科：设“不等式x²-ξx+1＜0对一切x∈[1，2]均成立”为事件D，试求事件D的概率．
组卷：39引用：1难度：0.3

（二）选考题：满分10分。请考生从22、23题中任选一题作答。如果多做则按所做的第一题计分。[选修4-4：坐标系与参数方程]（10分）

22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的一个顶点为P（0，1），且离心率为
3
2
．
（1）求椭圆C的方程；
（2）已知点Q坐标为（-2，0），直线y=2x+1与椭圆C交于A、B两点，求△ABQ的面积；
（3）若直线l：y=x+m与椭圆C交于M、N两点，且|PM|=|PN|，求m的值．
组卷：29引用：2难度：0.5

[选修4-5：不等式选讲]（10分）

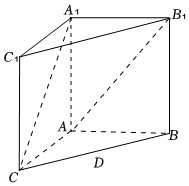23．如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=AC=4，AB=3，BC=5，点D是线段BC的中点．
（1）求证：AB⊥A₁C；
（2）求二面角D-CA₁-A的余弦值．
组卷：350引用：7难度：0.6

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． [ - π 2 ， 0 ]	B． [ - π 4 ， π 12 ]
C． [ - π 2 ，- π 4 ）， [ π 12 ， 5 π 12 ]	D． [ - π 4 ， π 12 ] ， [ 5 π 12 ， π 2 ]

A．（x-1）²+（y-2）²=4	B．（x-1）²+（y-3）²=9
C．（x-2）²+（y-2）²=4	D．（x-2）²+（y-3）²=9

2020-2021学年安徽省池州市高三（上）期末数学试卷（理科）

一、选择题：共12小题，每小题5分，满分60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．i为虚数单位，复数1+i1-2i在复平面内对应的点位于（ ）

2．已知函数f（x）=2cos（π4-3x），x∈[-π2，π2]，则f（x）的单调递增区间是（ ）

3．已知向量a，b，c满足|a|=|b|=2，|c|=23，且a+b+c=0，则cos〈a，b〉=（ ）

4．抛物线C：y2=2px（p＞0）的焦点为F，且抛物线C与椭圆x22+y2=1在第一象限的交点为A，若AF⊥x轴，则p=（ ）

5．已知集合A={x|x2+2x-15＜0}，B={x|x＞1}，则A∪B等于（ ）

6．设a=20.1，b=log20.1，c=cos0.1，则（ ）

7．已知sin（α+π3）=13，则cos（2α-π3）=（ ）

8．某品牌为了研究旗下某产品在淘宝、抖音两个平台的销售状况，统计了2021年7月到12月淘宝和抖音官方平台的月营业额（单位：万元），得到如图所示的折线图．下列说法错误的是（ ）

9．执行如图所示的程序框图，输出的结果为（ ）

10．已知a=0.52，b=20.5，c=log0.52，则a,b,c的大小关系为（ ）

11．已知双曲线C：x2-y224=1的两焦点分别是F1，F2，双曲线C1在第一象限部分有一点P，满足|PF1|+|PF2|=14．若圆C2与△PF1F2三边都相切，则圆C2的标准方程为（ ）

二、填空题：共4小题每小题5分，满分20分。

15．若实数x,y满足：x-y≤2x+y≥2x+3y≤6，则目标函数z=2x-y的最大值是 ．

16．若某正方体的外接球的表面积为12π，则这个正方体内切球的半径为．

三、解答题：满分60分。解答应写出文字说明，证明过程或演算步骤。第17-21题为必考题，每个试题考生都必须作答。第22、23题为选考题考生根据要求作答。（一）必考题：满分60分。

18．已知f（x）=|x+2|+|x-a|．（1）当a=1时，求不等式f（x）≥5的解集；（2）若f（x）＞2a恒成立，求实数a的取值范围．

19．设函数f（x）=x3-3ax+b（a≠0）在点（2，f（2））处与直线y=8相切．（1）求函数f（x）的解析式；（2）求函数f（x）的单调区间与极值．

20．在公差不为零的等差数列{an}和等比数列{bn}中，已知a1=1且a1=b1，a2=b2，a5=b3（1）求等差数列{an}，等比数列{bn}的通项公式（2）当Tn=1anaa+1，求数列{Tn}的前n项和．

（二）选考题：满分10分。请考生从22、23题中任选一题作答。如果多做则按所做的第一题计分。[选修4-4：坐标系与参数方程]（10分）

[选修4-5：不等式选讲]（10分）

23．如图，在直三棱柱ABC-A1B1C1中，AA1=AC=4，AB=3，BC=5，点D是线段BC的中点．（1）求证：AB⊥A1C；（2）求二面角D-CA1-A的余弦值．

1．i为虚数单位，复数
1
+
i
1
-
2
i
在复平面内对应的点位于（　　）

2．已知函数
f
（
x
）
=
2
cos
（
π
4
-
3
x
）
，
x
∈
[
-
π
2
，
π
2
]
，则f（x）的单调递增区间是（　　）

3．已知向量
a
，
b
，
c
满足
|
a
|
=
|
b
|
=
2
，
|
c
|
=
2
3
，且
a
+
b
+
c
=
0
，则
cos
〈
a
，
b
〉
=（　　）

4．抛物线C：y²=2px（p＞0）的焦点为F，且抛物线C与椭圆
x
2
2
+
y
2
=
1
在第一象限的交点为A，若AF⊥x轴，则p=（　　）

5．已知集合A={x|x²+2x-15＜0}，B={x|x＞1}，则A∪B等于（　　）

6．设a=2^0.1，b=log₂0.1，c=cos0.1，则（　　）

7．已知
sin
（
α
+
π
3
）
=
1
3
，则
cos
（
2
α
-
π
3
）
=（　　）

8．某品牌为了研究旗下某产品在淘宝、抖音两个平台的销售状况，统计了2021年7月到12月淘宝和抖音官方平台的月营业额（单位：万元），得到如图所示的折线图．下列说法错误的是（　　）

9．执行如图所示的程序框图，输出的结果为（　　）

10．已知a=0.5²，b=2^0.5，c=log_0.52，则a,b,c的大小关系为（　　）

11．已知双曲线C：x²-
y
2
24
=1的两焦点分别是F₁，F₂，双曲线C₁在第一象限部分有一点P，满足|PF₁|+|PF₂|=14．若圆C₂与△PF₁F₂三边都相切，则圆C₂的标准方程为（　　）

15．若实数x,y满足：
x
-
y
≤
2
x
+
y
≥
2
x
+
3
y
≤
6
，则目标函数z=2x-y的最大值是
．

16．若某正方体的外接球的表面积为12π，则这个正方体内切球的半径为
．

18．已知f（x）=|x+2|+|x-a|．
（1）当a=1时，求不等式f（x）≥5的解集；
（2）若f（x）＞2a恒成立，求实数a的取值范围．

19．设函数f（x）=x³-3ax+b（a≠0）在点（2，f（2））处与直线y=8相切．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间与极值．

20．在公差不为零的等差数列{a_n}和等比数列{b_n}中，已知a₁=1且a₁=b₁，a₂=b₂，a₅=b₃
（1）求等差数列{a_n}，等比数列{b_n}的通项公式
（2）当T_n=
1
a
n
a
a
+
1
，求数列{T_n}的前n项和．

23．如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=AC=4，AB=3，BC=5，点D是线段BC的中点．
（1）求证：AB⊥A₁C；
（2）求二面角D-CA₁-A的余弦值．