当前位置：试卷中心 > 试卷详情

2023-2024学年广东省普宁市勤建学校高二（上）第二次月考数学试卷

发布：2025/11/17 9:0:37

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．

1．若直线x+y-3=0与2x+ay-1=0垂直，则a=（　　）
A．-2 B．2 C．
1
2
D．
-
1
2
组卷：140引用：6难度：0.8
2．已知直线l：4x-3y+20=0，直线m：ax-3y=0与直线l平行，则直线l与m之间的距离为（　　）
A．
8
5
B．
12
5
C．4 D．2
组卷：33引用：2难度：0.7
3．在空间直角坐标系Oxyz中，点A（1，2，3）关于yOz平面对称的点的坐标为（　　）
A．（-1，2，3） B．（1，-2，3） C．（1，2，-3） D．（-1，-2，-3）
组卷：1035引用：7难度：0.8
4．已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，四点P₁（1，1），P₂（0，1），
P
3
（
-
1
，
3
2
）
，
P
4
（
1
，
3
2
）
中恰有三个点在椭圆C上，则这三个点是（　　）
A．P₁，P₂，P₃ B．P₁，P₂，P₄ C．P₁，P₃，P₄ D．P₂，P₃，P₄
组卷：37引用：2难度：0.7
5．若椭圆
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
上的点
（
2
，
5
3
）
到右准线的距离为
5
2
，过点M（0，1）的直线l与C交于两点A，B，且
AM
=
2
3
MB
，则l的斜率为（　　）
A．
1
3
B．
±
1
3
或
±
2
21
27
C．
±
1
2
D．
1
9
组卷：85引用：4难度：0.6
6．设
a
、
b
、
c
是空间向量，则以下说法中错误的是（　　）
A．
a
、
b
一定共面 B．
a
、
b
、
c
一定不共面
C．
a
•
b
=
b
•
a
D．
a
•
（
b
+
c
）
=
a
•
b
+
a
•
c
组卷：39引用：2难度：0.7
7．直线3x+my-2m=0平分圆C：x²+2x+y²-2y=0，则m=（　　）
A．
3
2
B．1 C．-1 D．-3
组卷：487引用：11难度：0.9
8．如果直线y=-
3
3
x+m曲线y=
1
-
x
2
有两个不同的公共点，那么实数m的取值范围是（　　）
A．[1，
2
3
3
） B．[
3
3
，
2
3
3
）
C．（-
3
3
，
2
3
3
] D．（-
2
3
3
，
2
3
3
）
组卷：171引用：8难度：0.7

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9．如图，在菱形ABCD中，AB=2，∠BAD=60°，将△ABD沿对角线BD翻折到△PBD位置，连结PC，则在翻折过程中，下列说法正确的是（　　）
A．PC与平面BCD所成的最大角为45°
B．存在某个位置，使得PB⊥CD
C．当二面角P-BD-C的大小为90°时，PC=
6
D．存在某个位置，使得B到平面PDC的距离为
3
组卷：348引用：12难度：0.6
10．已知直线l₁：x-y+m=0，l₂：2x+my-1=0，则下列结论正确的有（　　）
A．若l₁∥l₂，则m=-2
B．若l₁⊥l₂，则m=2
C．若l₁，l₂在x轴上的截距相等，则m=1
D．l₂的倾斜角不可能是l₁倾斜角的2倍
组卷：296引用：5难度：0.7
11．若
a
=
（
-
1
，
λ
，-
2
）
，
b
=
（
2
，-
1
，
1
）
，
a
与
b
的夹角为120°，则λ的值为（　　）
A．17 B．-17 C．-1 D．1
组卷：1556引用：26难度：0.9
12．关于椭圆3x²+4y²=12有以下结论，其中正确的有（　　）
A．离心率为
1
2
B．长轴长是2
3
C．焦点在y轴上
D．焦点坐标为（-1，0），（1，0）
组卷：215引用：7难度：0.6

三、填空题：本题共4小题，每小题5分，共20分．

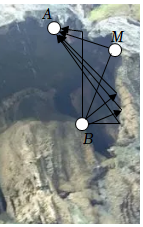13．甲、乙两名探险家在桂林山中探险，他们来到一个山洞，洞内是一个椭球形，截面是一个椭圆，甲、乙两人分别站在洞内如图所示的A、B两点处，甲站在A处唱歌时离A处有一定距离的乙在B处听得很清晰，原因在于甲、乙两人所站的位置恰好是洞内截面椭圆的两个焦点，符合椭圆的光学性质，即从一个焦点发出光经椭圆反射后经过另一个焦点．现已知椭圆：C：
x
2
100
+
y
2
36
=1上一点M，过点M作切线l,A，B两点为左、右焦点，cos∠AMB=-
1
4
，由光的反射性质：光的入射角等于反射角，则椭圆中心O到切线l的距离为
．
组卷：80引用：2难度：0.5
14．如果AC＜0，BC＞0，那么直线Ax+By+C=0不通过第
象限．
组卷：213引用：6难度：0.9
15．圆心在第二象限，半径为3，且与两条坐标轴均相切的圆的标准方程为
．
组卷：81引用：2难度：0.7
16．点A（2，2）关于直线2x-4y+9=0的对称点的坐标为
．
组卷：183引用：4难度：0.9

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17．已知函数f（x）=x²-4x+a+3，g（x）=mx+5-2m.
（Ⅰ）若y=f（x）在[-1，1]上存在零点，求实数a的取值范围；
（Ⅱ）当a=0时，若对任意的x₁∈[1，4]，总存在x₂∈[1，4]，使f（x₁）=g（x₂）成立，求实数m的取值范围；
（Ⅲ）若函数y=f（x）（x∈[t,4]）的值域为区间D，是否存在常数t,使区间D的长度为7-2t？若存在，求出所有t的值；若不存在，请说明理由（注：区间[p,q]的长度为q-p）．
组卷：198引用：9难度：0.5
18．已知直线l：x-y+3=0被圆C：（x-a）²+（y-2）²=4（a＞0）截得的弦长为
2
2
．
（1）求a的值；
（2）求过点（3，5）与圆相切的直线的方程．
组卷：1146引用：10难度：0.8
19．已知圆C的圆心在直线2x+y-4=0上，且与y轴相切于点O（0，0）．
（1）求圆C的方程；
（2）已知过点P（1，3）的直线l被圆C截得的弦长为
2
3
，求直线l的方程．
组卷：197引用：3难度：0.5
20．已知直线l₁：（m+2）x+（m²-3m）y+4=0和直线l₂：2mx+2（m-3）y+m+2=0（m∈R）．
（1）当m为何值时，直线l₁和l₂平行？
（2）当m为何值时，直线l₁和l₂重合？
组卷：119引用：3难度：0.7
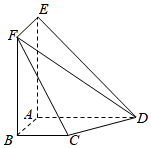21．如图所示，AE⊥平面ABCD，四边形AEFB为矩形，BC∥AD，BA⊥AD，AE=AD=2AB=2BC=4．
（1）求证：CF∥平面ADE；
（2）求平面CDF与平面AEFB所成锐二面角的余弦值．
组卷：520引用：17难度：0.4
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）经过点M（1，
2
2
），N（
2
，0）．
（1）求椭圆C的方程；
（2）已知直线l的倾斜角为锐角，l与圆x²+y²=
1
2
相切，与椭圆C交于A、B两点，且△AOB的面积为
2
3
，求直线l的方程．
组卷：266引用：3难度：0.6

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A． a 、 b 一定共面	B． a 、 b 、 c 一定不共面
C． a • b = b • a	D． a • （ b + c ） = a • b + a • c

A．[1， 2 3 3 ）	B．[ 3 3 ， 2 3 3 ）
C．（- 3 3 ， 2 3 3 ]	D．（- 2 3 3 ， 2 3 3 ）

2023-2024学年广东省普宁市勤建学校高二（上）第二次月考数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．

1．若直线x+y-3=0与2x+ay-1=0垂直，则a=（ ）

2．已知直线l：4x-3y+20=0，直线m：ax-3y=0与直线l平行，则直线l与m之间的距离为（ ）

3．在空间直角坐标系Oxyz中，点A（1，2，3）关于yOz平面对称的点的坐标为（ ）

4．已知椭圆C：x2a2+y2b2=1（a＞b＞0），四点P1（1，1），P2（0，1），P3（-1，32），P4（1，32）中恰有三个点在椭圆C上，则这三个点是（ ）

5．若椭圆C：x2a2+y2b2=1（a＞b＞0）上的点（2，53）到右准线的距离为52，过点M（0，1）的直线l与C交于两点A，B，且AM=23MB，则l的斜率为（ ）

6．设a、b、c是空间向量，则以下说法中错误的是（ ）

7．直线3x+my-2m=0平分圆C：x2+2x+y2-2y=0，则m=（ ）

8．如果直线y=-33x+m曲线y=1-x2有两个不同的公共点，那么实数m的取值范围是（ ）

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9．如图，在菱形ABCD中，AB=2，∠BAD=60°，将△ABD沿对角线BD翻折到△PBD位置，连结PC，则在翻折过程中，下列说法正确的是（ ）

10．已知直线l1：x-y+m=0，l2：2x+my-1=0，则下列结论正确的有（ ）

11．若a=（-1，λ，-2），b=（2，-1，1），a与b的夹角为120°，则λ的值为（ ）

12．关于椭圆3x2+4y2=12有以下结论，其中正确的有（ ）

三、填空题：本题共4小题，每小题5分，共20分．

14．如果AC＜0，BC＞0，那么直线Ax+By+C=0不通过第象限．

15．圆心在第二象限，半径为3，且与两条坐标轴均相切的圆的标准方程为 ．

16．点A（2，2）关于直线2x-4y+9=0的对称点的坐标为．

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

18．已知直线l：x-y+3=0被圆C：（x-a）2+（y-2）2=4（a＞0）截得的弦长为22．（1）求a的值；（2）求过点（3，5）与圆相切的直线的方程．

19．已知圆C的圆心在直线2x+y-4=0上，且与y轴相切于点O（0，0）．（1）求圆C的方程；（2）已知过点P（1，3）的直线l被圆C截得的弦长为23，求直线l的方程．

20．已知直线l1：（m+2）x+（m2-3m）y+4=0和直线l2：2mx+2（m-3）y+m+2=0（m∈R）．（1）当m为何值时，直线l1和l2平行？（2）当m为何值时，直线l1和l2重合？

21．如图所示，AE⊥平面ABCD，四边形AEFB为矩形，BC∥AD，BA⊥AD，AE=AD=2AB=2BC=4．（1）求证：CF∥平面ADE；（2）求平面CDF与平面AEFB所成锐二面角的余弦值．

22．已知椭圆C：x2a2+y2b2=1（a＞b＞0）经过点M（1，22），N（2，0）．（1）求椭圆C的方程；（2）已知直线l的倾斜角为锐角，l与圆x2+y2=12相切，与椭圆C交于A、B两点，且△AOB的面积为23，求直线l的方程．

1．若直线x+y-3=0与2x+ay-1=0垂直，则a=（　　）

2．已知直线l：4x-3y+20=0，直线m：ax-3y=0与直线l平行，则直线l与m之间的距离为（　　）

3．在空间直角坐标系Oxyz中，点A（1，2，3）关于yOz平面对称的点的坐标为（　　）

4．已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，四点P₁（1，1），P₂（0，1），
P
3
（
-
1
，
3
2
）
，
P
4
（
1
，
3
2
）
中恰有三个点在椭圆C上，则这三个点是（　　）

5．若椭圆
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
上的点
（
2
，
5
3
）
到右准线的距离为
5
2
，过点M（0，1）的直线l与C交于两点A，B，且
AM
=
2
3
MB
，则l的斜率为（　　）

6．设
a
、
b
、
c
是空间向量，则以下说法中错误的是（　　）

7．直线3x+my-2m=0平分圆C：x²+2x+y²-2y=0，则m=（　　）

8．如果直线y=-
3
3
x+m曲线y=
1
-
x
2
有两个不同的公共点，那么实数m的取值范围是（　　）

9．如图，在菱形ABCD中，AB=2，∠BAD=60°，将△ABD沿对角线BD翻折到△PBD位置，连结PC，则在翻折过程中，下列说法正确的是（　　）

10．已知直线l₁：x-y+m=0，l₂：2x+my-1=0，则下列结论正确的有（　　）

11．若
a
=
（
-
1
，
λ
，-
2
）
，
b
=
（
2
，-
1
，
1
）
，
a
与
b
的夹角为120°，则λ的值为（　　）

12．关于椭圆3x²+4y²=12有以下结论，其中正确的有（　　）

14．如果AC＜0，BC＞0，那么直线Ax+By+C=0不通过第
象限．

15．圆心在第二象限，半径为3，且与两条坐标轴均相切的圆的标准方程为
．

16．点A（2，2）关于直线2x-4y+9=0的对称点的坐标为
．

18．已知直线l：x-y+3=0被圆C：（x-a）²+（y-2）²=4（a＞0）截得的弦长为
2
2
．
（1）求a的值；
（2）求过点（3，5）与圆相切的直线的方程．

19．已知圆C的圆心在直线2x+y-4=0上，且与y轴相切于点O（0，0）．
（1）求圆C的方程；
（2）已知过点P（1，3）的直线l被圆C截得的弦长为
2
3
，求直线l的方程．

20．已知直线l₁：（m+2）x+（m²-3m）y+4=0和直线l₂：2mx+2（m-3）y+m+2=0（m∈R）．
（1）当m为何值时，直线l₁和l₂平行？
（2）当m为何值时，直线l₁和l₂重合？

21．如图所示，AE⊥平面ABCD，四边形AEFB为矩形，BC∥AD，BA⊥AD，AE=AD=2AB=2BC=4．
（1）求证：CF∥平面ADE；
（2）求平面CDF与平面AEFB所成锐二面角的余弦值．

22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）经过点M（1，
2
2
），N（
2
，0）．
（1）求椭圆C的方程；
（2）已知直线l的倾斜角为锐角，l与圆x²+y²=
1
2
相切，与椭圆C交于A、B两点，且△AOB的面积为
2
3
，求直线l的方程．