2022-2023学年浙江省宁波市余姚中学高二（上）月考数学试卷（10月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若直线过点（1，0），（4，

  3

  ），则此直线的倾斜角是（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：11引用：3难度：0.9

  解析

• 2．已知

  a

  ，

  b

  ，

  c

  ，

  d

  是四个非零向量，下列说法正确的是（　　）

  A． a • b b = a

  B． （ a • b ） 2 = a 2 • b 2

  C．如果 | a | ＞ | b | ， | c | ＞ | d | ，那么 | a • c | ＞ | b • d |

  D．如果 a • b = 0 ，那么 a ⊥ b
  组卷：8引用：2难度：0.8

  解析

• 3．已知一个样本，样本容量为10，平均数为15，方差为3，现从样本中去掉一个数据15，此时样本的平均数为

  x

  ，方差为s²，则（　　）

  A． x ＞ 15 ， s 2 ＜ 3

  B． x ＜ 15 ， s 2 ＞ 3

  C． x = 15 ， s 2 ＞ 3

  D． x = 15 ， s 2 ＜ 3
  组卷：343引用：3难度：0.7

  解析

• 4．在一次试验中，随机事件A，B满足

  P

  （

  A

  ）

  =

  P

  （

  B

  ）

  =

  2

  3

  ，则（　　）

  A．事件A，B一定互斥

  B．事件A，B一定不互斥

  C．事件A，B一定互相独立

  D．事件A，B一定不互相独立
  组卷：196引用：5难度：0.8

  解析

• 5．已知点A（2，-3），B（-3，-2）直线l过点P（1，1），且与线段AB相交，则直线l的斜率k的取值范围是（　　）

  A． （ - ∞ ，- 4 ] ∪ [ 3 4 ， + ∞ ）	B． （ - ∞ ，- 1 4 ] ∪ [ 3 4 ， + ∞ ）
  C． [ - 4 ， 3 4 ]	D． [ 3 4 ， 4 ]
  组卷：726引用：42难度：0.7

  解析

• 6．已知△ABC的顶点B（2，1），C（-6，3），其垂心为H（-3，2），则其顶点A的坐标为（　　）

  A．（-19，-62）

  B．（19，-62）

  C．（-19，62）

  D．（19，62）
  组卷：148引用：8难度：0.7

  解析

• 7．在二面角的棱上有两个点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，若AB=1，AC=2，BD=3，CD=2

  2

  ，则这个二面角的大小为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：609引用：6难度：0.5

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步䯅.

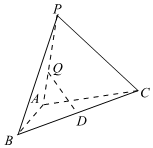• 21．如图，在△ABC中，AB=1，BC=2

  2

  ，B=

  π

  4

  ，将△ABC绕边AB翻转至△ABP，使面△ABP⊥面△ABC，D是BC的中点．
  （1）求二面角P-BC-A的平面角的余弦值；
  （2）设Q是线段PA上的动点，当PC与DQ所成角取得最小值时，求线段AQ的长度．
  组卷：154引用：2难度：0.5

  解析

• 22．已知f（x）=a•2^2x-2•2^x+1-a,x∈R，a∈R．
  （Ⅰ）解关于x的方程f（x）=（a-1）•4^x；
  （Ⅱ）设h（x）=2^-xf（x），a≥

  1

  2

  时，对任意x₁，x₂∈[-1，1]总有|h（x₁）-h（x₂）|≤

  a

  +

  1

  2

  成立，求a的取值范围．
  组卷：36引用：4难度：0.3

  解析