2023年湖北省咸宁市中考数学三模试卷
发布:2024/6/13 8:0:9
一.选择题(共8小题,每小题3分,共24分)
-
1.在实数
,36,32,0.1010010001…,227,π3,中,无理数有( )个.5组卷:207引用:4难度:0.7 -
2.在物联网时代的所有芯片中,0.000000014m芯片已成为需求的焦点.把它用科学记数法表示正确的是( )
组卷:228引用:7难度:0.7 -
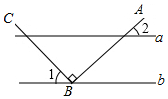 3.如图,a∥b,点B在直线b上,且AB⊥BC,∠1=42°,那么∠2的度数为( )组卷:281引用:4难度:0.8
3.如图,a∥b,点B在直线b上,且AB⊥BC,∠1=42°,那么∠2的度数为( )组卷:281引用:4难度:0.8 -
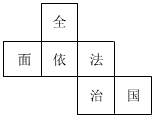 4.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么原正方体中,与“国”字所在面相对的面上的汉字是( )组卷:273引用:6难度:0.7
4.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么原正方体中,与“国”字所在面相对的面上的汉字是( )组卷:273引用:6难度:0.7 -
5.下列说法正确的是( )
组卷:459引用:12难度:0.7 -
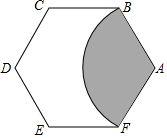 6.如图,以正六边形ABCDEF的顶点A为圆心,AB为半径作⊙A,与正六边形ABCDEF重合的扇形部分恰好是一个圆锥侧面展开图,则该圆锥的底面半径与母线长之比为( )组卷:442引用:5难度:0.7
6.如图,以正六边形ABCDEF的顶点A为圆心,AB为半径作⊙A,与正六边形ABCDEF重合的扇形部分恰好是一个圆锥侧面展开图,则该圆锥的底面半径与母线长之比为( )组卷:442引用:5难度:0.7 -
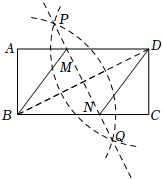 7.如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于BD的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC交于点M、N,连接BM、DN.若AD=4,AB=2.则四边形MBND的周长为( )12组卷:1209引用:11难度:0.4
7.如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于BD的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC交于点M、N,连接BM、DN.若AD=4,AB=2.则四边形MBND的周长为( )12组卷:1209引用:11难度:0.4 -
8.对于抛物线y=ax2+4ax-m(a≠0)与x轴的交点为A(-1,0),B(x2,0),则下列说法:
①一元二次方程ax2+4ax-m=0的两根为x1=-1,x2=-3;
②原抛物线与y轴交于点C,CD∥x轴交抛物线于D点,则CD=4;
③点E(1,y1)、点F(-4,y2)在原抛物线上,则y1>y2;
④抛物线y=-ax2-4ax+m与原抛物线关于x轴对称.其中正确的有( )组卷:841引用:5难度:0.4
三.解答题(共8小题,共72分)
-
23.在△ABC中,∠ACB=90°,
=m,D是边BC上一点,将△ABD沿AD折叠得到△AED,连接BE.ACBC
(1)特例发现:如图1,当m=1,AE落在直线AC上时.求证:∠DAC=∠EBC;
(2)类比探究
如图2,当m≠1,AE与边BC相交时,在AD上取一点G,使∠ACG=∠BCE,CG交AE于点H.探究的值(用含m的式子表示),并写出探究过程;CGCE
(3)拓展运用
在(2)条件下,当,D是BC的中点时,若EB•EH=6,直接写出CG的长.m=22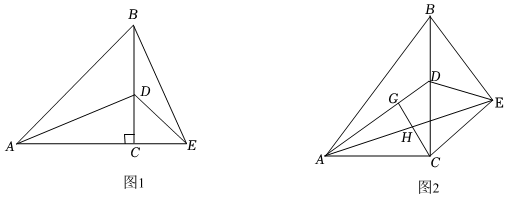 组卷:961引用:4难度:0.3
组卷:961引用:4难度:0.3 -
24.如图1,在平面直角坐标系中,直线
分别与x轴,y轴交于点A、B(0,1),抛物线y=34x+1经过点B,且与直线y=-12x2+bx+c的另一个交点为C(-4,n).y=34+1
(1)求抛物线的解析式;
(2)如图2,点D是抛物线上一动点,且点D的横坐标为t(-4<t<0),过点D作y轴的平行线,交x轴于点G,交BC于点E,作DF⊥BC于点F,若Rt△DEF的周长为l,求l与t的函数关系式以及l的最大值;
(3)抛物线的对称轴上是否存在一点P,使得△BCP为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.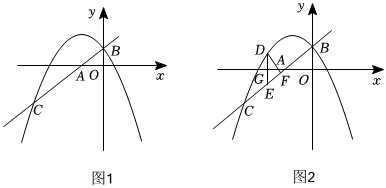 组卷:106引用:1难度:0.4
组卷:106引用:1难度:0.4


