当前位置：试卷中心 > 试卷详情

2020-2021学年广东省珠海市艺术高级中学高一（下）期中数学试卷

发布：2024/7/7 8:0:9

1．已知a∈R，若a-1+（a-2）i（i为虚数单位）是实数，则a=（　　）
A．1 B．-1 C．2 D．-2
组卷：2852引用：11难度：0.8
解析
2．复平面上矩形ABCD的四个顶点中，A、B、C所对应的复数分别为2+3i、3+2i、-2-3i,则D点对应的复数是（　　）
A．-2+3i B．-3-2i C．2-3i D．3-2i
组卷：159引用：18难度：0.9
解析
3．已知向量
a
=（m,-2）与
b
=（4，n）共线，则m•n的值为（　　）
A．8 B．-8 C．4 D．-4
组卷：221引用：2难度：0.8
解析
4．已知
a
、
b
均为单位向量，它们的夹角为60°，那么
|
a
+
b
|
=（　　）
A．3 B．2 C．4 D．
3
组卷：149引用：12难度：0.9
解析
5．在△ABC中，a=8，B=60°，C=75°，则b等于（　　）
A．
4
2
B．
4
3
C．
4
6
D．4
组卷：69引用：2难度：0.9
解析
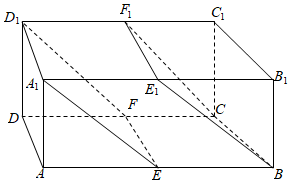6．如图所示，设E，F，E₁，F₁分别是长方体ABCD-A₁B₁C₁D₁的棱AB，CD，A₁B₁，C₁D₁的中点，则平面EFD₁A₁与平面BCF₁E₁的位置关系是（　　）
A．平行 B．相交 C．异面 D．不确定
组卷：141引用：8难度：0.9
解析
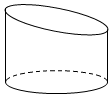7．如图，一个底面半径为2的圆柱被一平面所截，截得的几何体的最短和最长母线长分别为2和3，则该几何体的体积为（　　）
A．5π B．6π C．20π D．10π
组卷：175引用：4难度：0.6
解析

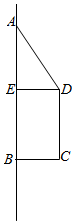21．如图，梯形ABCD满足AB∥CD，
∠
ABC
=
90
°
，
AB
=
2
3
，BC=1，∠BAD=30°，现将梯形ABCD绕AB所在直线旋转一周，所得几何体记为Ω．
（1）求Ω的体积V；
（2）求Ω的表面积S．
组卷：657引用：8难度：0.5
解析
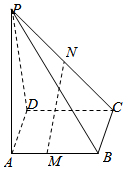22．如图，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点；
（1）求证：MN∥平面PAD．
（2）在PB上确定一点Q，使平面MNQ∥平面PAD．
组卷：2571引用：18难度：0.5
解析

1．已知a∈R，若a-1+（a-2）i（i为虚数单位）是实数，则a=（ ）