2023年黑龙江齐黑大地区中考数学模拟试卷（二）

一、选择题（每小题3分，满分30分)

• 1．下列各数中，绝对值最大的数是（　　）

  A．4

  B．-5

  C．0

  D．-1
  组卷：556引用：12难度：0.9

  解析

• 2．下列图案中，不是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：791引用：49难度：0.9

  解析

• 3．下列运算正确的是（　　）

  A．a6÷a2=a2

  B． 3 - 27 - 3 = 2 3

  C． 5 a - 3 = 1 5 a 3

  D．（π-3）0=1
  组卷：21引用：1难度：0.7

  解析

• 4．甲、乙、丙、丁四名运动员进行百米测试，每人8次测试成绩的平均数都是13.4秒，方差分别为S_甲²=0.73，S_乙²=0.75，S_丙²=0.69，S_丁²=0.68，则这四名运动员百米成绩最稳定的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：214引用：9难度：0.7

  解析

• 5．一个几何体由若干个大小相同的小立方块搭成，如图分别是它的主视图和俯视图，若该几何体所用小立方块的个数为n个，则n的最小值为（　　）

  A．9

  B．11

  C．12

  D．13
  组卷：227引用：5难度：0.7

  解析

• 6．从甲，乙，丙三人中任选两名代表，甲被选中的可能性是（　　）

  A． 2 3

  B． 1 3

  C． 1 4

  D． 1 5
  组卷：482引用：3难度：0.5

  解析

• 7．如图，在锐角△ABC中，BD，CE分别是AC、AB边上的高，且BD与CE相交于点O，若∠A=50°，∠BOC的度数为（　　）

  A．120°

  B．125°

  C．130°

  D．135°
  组卷：350引用：5难度：0.7

  解析

• 8．如图，已知直线l是线段AB的中垂线，l与AB相交于点C，点D是位于直线AB下方的l上的一动点（点D不与C重合），连接AD，BD．过点A作AE∥BD，过点B作BE⊥AE，AE与BE相交于点E．若AB=6，设AD=x,AE=y,则y关于x的函数关系用图象可以大致表示为（　　）

  A．

  B．

  C．

  D．
  组卷：522引用：6难度：0.4

  解析

三、解答题（共69分）

• 23．综合与实践如图，正方形ACBF与正方形CDGE有公共顶点C，AC=3，CD=2，连接AD，BE．
  
  （1）如图①，当点E，G在正方形ACBF内时，线段BE与AD的数量关系是

  ，位置关系是

  ；
  （2）把正方形CDGE绕点C旋转到如图②的位置，（1）中的结论还成立吗？说明理由；
  （3）把正方形CDGE绕点C在平面内自由旋转．
  ①当A，E，D三点在同一条直线上时，AE的长是

  ；
  ②旋转过程中，|AE-AD|的最大值为

  ．
  组卷：59引用：4难度：0.3

  解析

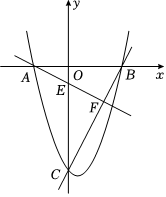• 24．综合与探究
  如图，抛物线y=ax²+bx+c与x轴交于点A、点B，与y轴交于点C，直线y=2x-6与抛物线交于点B、点C，直线y=-

  1

  2

  x-1与抛物线交于点A，与y轴交于点E，与直线y=2x-6交于点F．
  （1）求抛物线的解析式；
  （2）已知点M（m,n）在抛物线上，当-4≤m≤2时，直接写出n的取值范围；
  （3）H是直线CB上一点，若S_△ECH=2S_△ECF，求点H的坐标；
  （4）P是x轴上一点，Q是平面内任意一点，是否存在以B，C，P，Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
  组卷：67引用：1难度：0.2

  解析