2023年湖北省随州市广水市中考数学模拟试卷

一、选择题：（本大题共10个小题最小的是（）

• 1．在实数0，-

  5

  ，

  6

  ，-2中，最小的是（　　）

  A．-2

  B．- 5

  C．0

  D． 6
  组卷：80引用：2难度：0.8

  解析

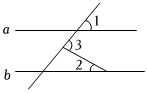• 2．如图，a∥b,∠3=80°，∠2=30°，则∠1的度数是（　　）

  A．30°

  B．40°

  C．50°

  D．80°
  组卷：1790引用：12难度：0.7

  解析

• 3．在数轴上表示不等式组

  x + 2 ＞ 0

  x ≤ 1

  的解，其中正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：405引用：10难度：0.9

  解析

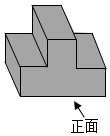• 4．如图所示几何体，其俯视图大致为（　　）

  A．

  B．

  C．

  D．
  组卷：238引用：4难度：0.8

  解析

• 5．下表是甲、乙、丙、丁四名射击运动员在一次预选赛中的射击成绩：
  

  	甲	乙	丙	丁
  平均环数	8	9	9	8
  方差	1	1	1.2	1.3

  则成绩较好且状态稳定的运动员是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：286引用：4难度：0.7

  解析

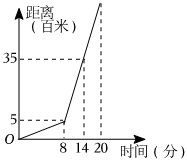• 6．某天早上小明上学，先步行一段路，因时间紧，他又改乘出租车，结果到校时还是迟到了3分钟，其行程情况如图，若他出门时直接乘出租车（两次车速相同），则正确的判断是（　　）
  ​

  A．仍会迟到3分钟到校	B．刚好按时到校
  C．可以提前4分钟到	D．可以提前3分钟到校
  组卷：90引用：1难度：0.7

  解析

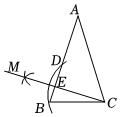• 7．如图，在△ABC中，AB=AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于

  1

  2

  BD

  长为半径画弧，两弧相交于点M，作射线CM交AB于点E，若AE=5，BE=1，则EC的长度为（　　）

  A．3

  B． 10

  C． 11

  D． 2 3
  组卷：474引用：10难度：0.5

  解析

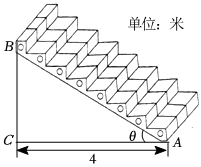• 8．一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，BA与CA的夹角为θ．现要在楼梯上铺一条地毯，已知CA=4米，楼梯宽度3米，则地毯的面积至少需要（　　）
  ​

  A． 4 sinθ 米2	B．（4+4tanθ）米2
  C． 3 （ 4 + 4 tanθ ） 米2	D．3（4+4tanθ）米2
  组卷：642引用：5难度：0.7

  解析

三、解答题（共8小题，满分72分）

• 23．定义：长宽比为

  n

  ：1（n为正整数）的矩形称为

  n

  矩形．下面，我们通过折叠的方式折出一个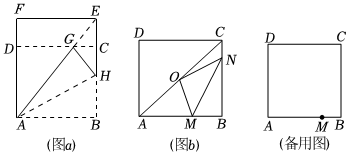

  2

  矩形，如图a所示．
  ​
  操作1：将正方形ABEF沿过点A的直线折叠，使折叠后的点B落在对角线AE上的点G处，折痕为AH．
  操作2：将FE沿过点G的直线折叠，使点F点E分别落在边AF，BE上，折痕为CD．
  （1）证明：四边形ABCD为

  2

  矩形；
  （2）点M在直线AB上一动点．
  ①如图b,O是对角线AC的中点，若点N在边BC上，OM⊥ON，连接MN．求tan∠OMN的值；
  ②若AM=AD，点N在边BC上，当△DMN的周长最小时，求

  CN

  NB

  的值；
  ③连接CM，作BR⊥CM，垂足为R．若AB=4，则DR的最大值=

  ．
  组卷：145引用：1难度：0.1

  解析

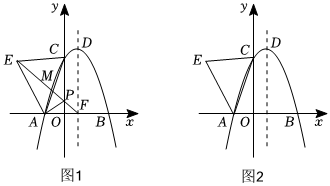• 24．如图1，抛物线y=ax²+bx+c（a≠0）与x轴、y轴分别交于A，B，C三点，B（3，0），A（-1，0），C（0，

  3

  ），抛物线的对称轴DF与抛物线交于点D，与x轴交于点F，以AC为边作等边三角形ACE，点E在第二象限．
  ​（1）求抛物线的解析式；
  （2）连接EF交AC于点M，交y轴于点P，连接AP，求点P的坐标；
  （3）在（2）的条件下，如图2，若等边三角形ACE沿x轴方向平移，点Q为平面内一点，在平移过程中是否存在点Q，使得以点A，D，E，Q为顶点的四边形是菱形？若存在，请直接写出点E的坐标；若不存在，请说明理由
  组卷：37引用：1难度：0.2

  解析