2023年浙江省温州市鹿城区绣山中学中考数学二模试卷
发布：2024/5/31 8:0:9
一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）
-
1．在4，-2，0，
四个数中，最小的为（ ）13组卷：164引用：5难度：0.9 -
2．2023年2月10日，神舟十五号航天员乘组圆满完成了首次出舱任务，据了解，这艘飞船的时速为每小时28000千米，28000千米用科学记数法表示应为（ ）
组卷：109引用：7难度：0.8 -
3．下列各图形中，经过折叠能围成一个立方体的为（ ）
组卷：229引用：5难度：0.8 -
4．不等式3x-2＜4的解集在数轴上表示正确的为（ ）
组卷：144引用：2难度：0.7 -
5．一次对若干名青少年进行最喜爱的运动项目的问卷调查，得到如图的统计图．若最喜爱足球的人数比最喜爱游泳的人数多20人，则这次问卷调查的总人数为（ ）
组卷：104引用：2难度：0.7 -
6．化简
的结果为（ ）a2a-1-aa-1组卷：329引用：4难度：0.6 -
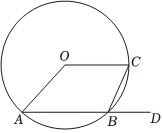7．如图，AB，BC为⊙O的两条弦，连结OA，OC，点D为AB的延长线上一点．若∠CBD=65°，则∠AOC为（ ）
组卷：160引用：2难度：0.7 -
8．中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两；马二匹、牛五头，共价三十八两．问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为 （ ）
组卷：731引用：8难度：0.8
三、解答题（本题有8小题，共80分）
-
23．根据以下素材，探索完成任务．
探究遮阳伞下的影子长度 素材1 图1是某款自动旋转遮阳伞，伞面完全张开时张角呈180°，图2是其侧面示意图．已知支架AB长为2.5米，且垂直于地面BC，悬托架AE=DE=0.5米，点E固定在伞面上，且伞面直径DF是DE的4倍．当伞面完全张开时，点D，E，F始终共线．为实现遮阳效果最佳，伞面装有接收器可以根据太阳光线的角度变化，自动调整手柄D沿着AB移动，以保证太阳光线与DF始终垂直．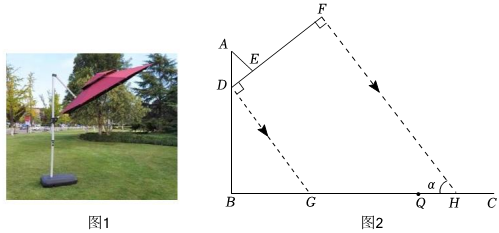 
素材2 某地区某天下午不同时间的太阳高度角α（太阳光线与地面的夹角）参照表： 时刻 12点 13点 14点 15点 16点 17点 太阳高度（度） 90 75 60 45 30 15 参考数据： ．3≈1.7，2≈1.4素材3 小明坐在露营椅上的高度（头顶到地面的距离）约为1米，如图2，小明坐的位置记为点Q． 问题解决 任务1 确定影子长度 某一时刻测得BD=1.7米．请求出此时影子GH的长度 任务2 判断是否照射到 这天14点，小明坐在离支架3米处的Q点，请判断此时小明是否会被太阳光照射到？ 任务3 探究合理范围 小明打算在这天14：00-15：00露营休息，为保证小明全程不被太阳光照射到，请计算BQ的取值范围． 组卷：1603引用：7难度：0.3 -
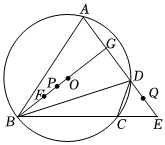24．如图，在圆内接四边形ABCD中，AD，BC的延长线交于点E，连结BO并延长交AD于点G，连结BD．已知BD=AB，∠CDE=3∠CBD，，BO=5．DE=154
（1）求证：∠GBD=∠CBD．
（2）求OG与GD的长．
（3）F是BO中点，动点P在FG上从点F向终点G匀速运动，同时动点Q在AE上从点E向终点A匀速运动．当点Q在点D处时，点P在点O处，设QE=x,PG=y.
①求y关于x的表达式．
②连结PQ，当直线PQ与△BCD的某一边所在的直线垂直时，记垂足为点M，求QM的值．组卷：490引用：6难度：0.3
