2022-2023学年浙江省金华一中高二（上）段考数学试卷（12月份）

一、选择题：（本题共7小题，每小题5分，40分．在每小题只有一项符合题目要求）

• 1．直线x+y-1=0与直线x+y+1=0的位置关系是（　　）

  A．垂直

  B．平行

  C．相交

  D．重合
  组卷：4引用：2难度：0.8

  解析

• 2．已知m,n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（　　）

  A．若m⊥α，m⊥β，则α⊥β	B．若α⊥γ，β⊥γ，则α∥β
  C．若m∥α，m∥β，则α∥β	D．若m⊥α，n∥α，则m⊥n
  组卷：98引用：10难度：0.9

  解析

• 3．已知直线l过点P（2，3），且与x,y轴的正半轴分别交于A、B两点，若△AOB的面积为12（O为坐标原点），则直线l的截距式方程为（　　）

  A． x 4 + y 6 = 1	B． x 8 + y 12 = 1
  C． x 13 2 + y 13 3 = 1	D． x 6 + y 4 = 1
  组卷：13引用：1难度：0.7

  解析

• 4．已知双曲线

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =1（a＞0，b＞0），其中一条渐近线的倾斜角为

  π

  6

  ，则双曲线的离心率为（　　）

  A． 2 3 3

  B． 3

  C．2

  D． 2 3
  组卷：91引用：4难度：0.8

  解析

• 5．一个正四面体的棱长为2，则这个正四面体的外接球的体积为（　　）

  A． 6 π

  B．2π

  C．3π

  D． 2 2 π
  组卷：57引用：1难度：0.5

  解析

• 6．设倾斜角为α的直线l经过抛物线C：y²=2px（p＞0）的焦点F，与抛物线C交于A、B两点，设A在x轴上方，点B在x轴上方．若

  |

  AF

  |

  |

  BF

  |

  =

  2

  ，则cosα的值为（　　）

  A． 1 3

  B． 1 2

  C． 2 3

  D． 2 2 3
  组卷：17引用：1难度：0.4

  解析

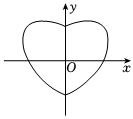• 7．数学中有许多形状优美、寓意美好的曲线，曲线C：x²+y²=1+|x|y就是其中之一（如图）．给出下列三个结论：
  ①曲线C恰好经过6个整点（即横、纵坐标均为整数的点）；
  ②曲线C上任意一点到原点的距离都不超过

  2

  ；
  ③曲线C关于x轴对称．
  其中，所有正确结论的序号是（　　）

  A．①

  B．②

  C．①②

  D．①②③
  组卷：29引用：2难度：0.7

  解析

四、解答题：（本题共6小题，共70分．其中17题10分，其余每题均12分．）

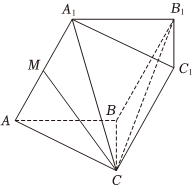• 20．如图，在三棱柱ABC-A₁B₁C₁中，AA₁=AB=AC=BC=2，∠A₁AB=60°，A₁C=3，点M为线段A₁A的中点．
  （1）求证：AB⊥A₁C；
  （2）求二面角A₁-AB-C的大小；
  （3）求三棱锥M-A₁B₁C的体积．
  组卷：13引用：2难度：0.5

  解析

• 21．如图所示，M、D分别为椭圆

  x

  2

  a

  2

  +

  y

  2

  =

  1

  （

  a

  ＞

  1

  ）

  的左、右顶点，离心率为

  3

  2

  ．
  
  （1）求椭圆的标准方程；
  （2）过M点作两条互相垂直的直线MA，MB与椭圆交于A，B两点，求△DAB面积的最大值．
  组卷：294引用：8难度：0.5

  解析