当前位置：试卷中心 > 试卷详情

2022-2023学年河南省TOP二十名校高一（下）调研数学试卷（5月份）

发布：2025/11/12 13:0:30

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若复数z满足（1-2i）z=2，则z的虚部为（　　）
A．
2
5
B．
-
2
5
C．
4
5
D．
-
4
5
组卷：89引用：3难度：0.8
2．A为三角形ABC的一个内角．若sinA+cosA=
12
25
，2sinBcosC=sinA，则这个三角形的形状不可能为（　　）
A．锐角三角形 B．钝角三角形
C．等腰且钝角三角形 D．等腰三角形
组卷：17引用：0难度：0.9
3．△ABC中∠C=90°，AC=2，P为线段BC上任一点，则
AP
•
AC
=（　　）
A．2 B．4 C．8 D．不确定
组卷：111引用：3难度：0.8
4．已知a,b,c为三条不同的直线，α，β，γ为三个不同的平面，则下列说法正确的是（　　）
A．若a∥b,b⊂α，则a∥α
B．若a⊂α，b⊂β，a∥b,则α∥β
C．若α∥β，a∥α，则a∥β
D．若α∩β=a,β∩γ=b,α∩γ=c,a∥b,则b∥c
组卷：538引用：11难度：0.7
5．
AD
+
DC
-
AB
等于（　　）
A．
BC
B．
AD
C．
AB
D．
DA
组卷：364引用：4难度：0.8
6．古希腊著名数学家欧几里德在《几何原本》一书中定义了圆锥与直角圆锥这两个概念：固定直角三角形的一条直角边，旋转直角三角形到开始位置，所形成的图形称为圆锥；如果固定的直角边等于另一直角边时，所形成的圆锥称为直角圆锥，则直角圆锥的侧面展开图（为一扇形）的圆心角的大小为（　　）
A．
π
2
B．
2
π
C．
3
2
π
D．与直角圆锥的母线长有关
组卷：28引用：3难度：0.7
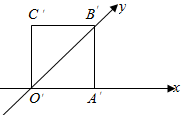7．如图，正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图，则原图的周长是（　　）
A．8cm B．6cm C．2（1+
3
）cm D．2（1+
2
）cm
组卷：883引用：44难度：0.9
8．已知复数Z=（-4+i）i,则复数Z在复平面内对应的点在第（　　）象限．
A．一 B．二 C．三 D．四
组卷：40引用：2难度：0.8

二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9．在长方体ABCD-A₁B₁C₁D₁中，已知AB=BC=3，AA₁=2，P，Q分别为A₁D₁，D₁C₁的中点，S为棱BC的三等分点，BS=1，过P，Q，S三点作一个平面α与C₁C，AB，A₁A分别交于点R，M，N，即得到一个截面PQRSMN，则（　　）
A．PQ∥MS
B．AN=CR
C．MN与平面ABCD所成的角的正切值为
4
7
D．点A到截面α的距离为1
组卷：33引用：4难度：0.5
10．已知△ABC的内角A，B，C所对的边分别是a,b,c,则下列命题正确的是（　　）
A．若sinA＞sinB，则a＞b
B．若a²+b²-c²＜0，则△ABC是钝角三角形
C．若acosA=bcosB，则△ABC为等腰三角形
D．若bcosC+ccosB=asinA，则△ABC为直角三角形
组卷：63引用：2难度：0.5
11．如果一个复数的实部和虚部相等，则称这个复数为“等部复数”．若复数z=a+2i（a∈R）为“等部复数”，则（　　）
A．a=2
B．|z|=4
C．
z
=
2
-
2
i
D．复数（a-2）+（a²-2）i是纯虚数
组卷：17引用：0难度：0.8
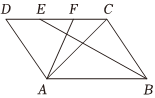12．如图，在平行四边形ABCD中，E、F分别是CD边上的两个三等分点，则下列选项正确的有（　　）
A．
EF
=
1
3
AB
B．
AD
+
DC
=
AB
+
BC
C．
BE
=
CB
-
CE
D．
AF
=
2
3
AD
+
1
3
AC
组卷：158引用：6难度：0.7

三、填空题：本题共4小题，每小题5分，共20分.

13．如果一条直线垂直于平面内的：①三角形的两条边；②圆的两条弦；③平行四边形的一组邻边；④梯形的两腰，其中能说明直线与平面垂直的有
．（只填序号）
组卷：15引用：1难度：0.7
14．△ABC中，若sinA=2sinB，AC=2，则BC=
．
组卷：73引用：11难度：0.7
15．已知向量
a
=
（
1
，
2
，-
1
）
与
b
=
（
m
,
m
+
2
，
1
）
垂直，则实数m的值为
．
组卷：14引用：1难度：0.8
16．一个正四棱锥和一个正方体，它们有半径相同的内切球，记正四棱锥的体积为V₁，正方体体积为V₂，且V₁=kV₂，则实数k的最大值为

．
组卷：18引用：0难度：0.9

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17．如图，三棱柱ABC-A₁B₁C₁中，侧面BB₁C₁C为菱形，B₁C的中点为O，AC=AB₁．

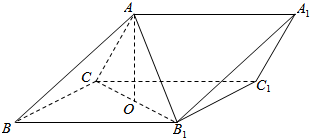
（1）文字叙述平面与平面垂直判定定理；
（2）求证：平面ABO⊥平面ACB₁．
组卷：30引用：1难度：0.3
18．在△ABC中，角A，B，C的对边分别为a,b,c,已知
（
a
+
b
）
（
sin
A
-
sin
B
）
=
（
3
a
-
c
）
sin
C
．
（1）求角B；
（2）若
C
=
2
π
3
，
a
=
3
，求BC边上中线的长．
组卷：58引用：2难度：0.6
19．在①acosB-bcosA=c-b,②tanA+tanB+tanC-
3
tanBtanC=0，③△ABC的面积为
1
2
a（bsinB+csinC-asinA），这三个条件中任选一个，补充在下面问题中，并加以解答．
在△ABC中，角A，B，C所对的边分别为a,b,c,且_____．
（1）求角A；
（2）若a=8，△ABC的内切圆半径为
3
，求△ABC的面积．
组卷：482引用：8难度：0.5
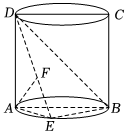20．如图，圆柱的轴截面ABCD是正方形，点E在底面的圆周上，AF⊥DE，F是垂足．
（1）求证：AF⊥DB；
（2）求将△ABD绕AD旋转一周所得几何体的表面积和圆柱表面积之比；
（32）如果圆柱与三棱锥D-ABE的体积比等于3π，求直线DE与平面ABCD所成的角．
组卷：60引用：1难度：0.4
21．已知向量
a
=
（
2
，
1
）
，
b
=
（
sinα
，
2
cosα
）
．
（1）若
α
=
3
π
4
，求证：
a
⊥
b
；
（2）若向量
a
，
b
共线，求tanα．
组卷：17引用：1难度：0.5
22．蜂房是自然界最神奇的“建筑”之一，如图1所示．蜂房结构是由正六棱柱截去三个相等的三棱锥H-ABC，J-CDE，K-EFA，再分别以AC，CE，EA为轴将△ACH，△CEJ，△EAK分别向上翻转180°，使H，J，K三点重合为点S所围成的曲顶多面体（下底面开口），如图2所示．蜂房曲顶空间的弯曲度可用曲率来刻画，定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和，而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和（多面体的面角是多面体的面的内角，用弧度制表示）．例如：正四面体在每个顶点有3个面角，每个面角是
π
3
，所以正四面体在各顶点的曲率为
2
π
-
3
×
π
3
=
π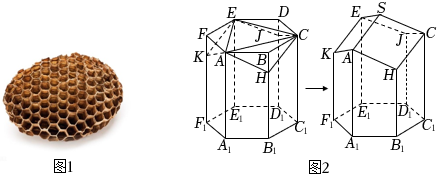
．

（1）求蜂房曲顶空间的弯曲度；
（2）若正六棱柱底面边长为1，侧棱长为2，设BH=x
（i）用x表示蜂房（图2右侧多面体）的表面积S（x）；
（ii）当蜂房表面积最小时，求其顶点S的曲率的余弦值．
组卷：171引用：5难度：0.4

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．锐角三角形	B．钝角三角形
C．等腰且钝角三角形	D．等腰三角形

A． EF = 1 3 AB	B． AD + DC = AB + BC
C． BE = CB - CE	D． AF = 2 3 AD + 1 3 AC

2022-2023学年河南省TOP二十名校高一（下）调研数学试卷（5月份）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若复数z满足（1-2i）z=2，则z的虚部为（ ）

2．A为三角形ABC的一个内角．若sinA+cosA=1225，2sinBcosC=sinA，则这个三角形的形状不可能为（ ）

3．△ABC中∠C=90°，AC=2，P为线段BC上任一点，则AP•AC=（ ）

4．已知a,b,c为三条不同的直线，α，β，γ为三个不同的平面，则下列说法正确的是（ ）

5．AD+DC-AB等于（ ）

7．如图，正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图，则原图的周长是（ ）

8．已知复数Z=（-4+i）i,则复数Z在复平面内对应的点在第（ ）象限．

二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9．在长方体ABCD-A1B1C1D1中，已知AB=BC=3，AA1=2，P，Q分别为A1D1，D1C1的中点，S为棱BC的三等分点，BS=1，过P，Q，S三点作一个平面α与C1C，AB，A1A分别交于点R，M，N，即得到一个截面PQRSMN，则（ ）

10．已知△ABC的内角A，B，C所对的边分别是a,b,c,则下列命题正确的是（ ）

11．如果一个复数的实部和虚部相等，则称这个复数为“等部复数”．若复数z=a+2i（a∈R） 为“等部复数”，则（ ）

12．如图，在平行四边形ABCD中，E、F分别是CD边上的两个三等分点，则下列选项正确的有（ ）

三、填空题：本题共4小题，每小题5分，共20分.

13．如果一条直线垂直于平面内的：①三角形的两条边；②圆的两条弦；③平行四边形的一组邻边；④梯形的两腰，其中能说明直线与平面垂直的有．（只填序号）

14．△ABC中，若sinA=2sinB，AC=2，则BC=．

15．已知向量a=（1，2，-1）与b=（m,m+2，1）垂直，则实数m的值为 ．

16．一个正四棱锥和一个正方体，它们有半径相同的内切球，记正四棱锥的体积为V1，正方体体积为V2，且V1=kV2，则实数k的最大值为 ．

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17．如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，AC=AB1．（1）文字叙述平面与平面垂直判定定理；（2）求证：平面ABO⊥平面ACB1．

18．在△ABC中，角A，B，C的对边分别为a,b,c,已知（a+b）（sinA-sinB）=（3a-c）sinC．（1）求角B；（2）若C=2π3，a=3，求BC边上中线的长．

21．已知向量a=（2，1），b=（sinα，2cosα）．（1）若α=3π4，求证：a⊥b；（2）若向量a，b共线，求tanα．

1．若复数z满足（1-2i）z=2，则z的虚部为（　　）

2．A为三角形ABC的一个内角．若sinA+cosA=
12
25
，2sinBcosC=sinA，则这个三角形的形状不可能为（　　）

3．△ABC中∠C=90°，AC=2，P为线段BC上任一点，则
AP
•
AC
=（　　）

4．已知a,b,c为三条不同的直线，α，β，γ为三个不同的平面，则下列说法正确的是（　　）

5．
AD
+
DC
-
AB
等于（　　）

7．如图，正方形O'A'B'C'的边长为1cm,它是水平放置的一个平面图形的直观图，则原图的周长是（　　）

8．已知复数Z=（-4+i）i,则复数Z在复平面内对应的点在第（　　）象限．

9．在长方体ABCD-A₁B₁C₁D₁中，已知AB=BC=3，AA₁=2，P，Q分别为A₁D₁，D₁C₁的中点，S为棱BC的三等分点，BS=1，过P，Q，S三点作一个平面α与C₁C，AB，A₁A分别交于点R，M，N，即得到一个截面PQRSMN，则（　　）

10．已知△ABC的内角A，B，C所对的边分别是a,b,c,则下列命题正确的是（　　）

11．如果一个复数的实部和虚部相等，则称这个复数为“等部复数”．若复数z=a+2i（a∈R）为“等部复数”，则（　　）

12．如图，在平行四边形ABCD中，E、F分别是CD边上的两个三等分点，则下列选项正确的有（　　）

13．如果一条直线垂直于平面内的：①三角形的两条边；②圆的两条弦；③平行四边形的一组邻边；④梯形的两腰，其中能说明直线与平面垂直的有
．（只填序号）

14．△ABC中，若sinA=2sinB，AC=2，则BC=
．

15．已知向量
a
=
（
1
，
2
，-
1
）
与
b
=
（
m
,
m
+
2
，
1
）
垂直，则实数m的值为
．

16．一个正四棱锥和一个正方体，它们有半径相同的内切球，记正四棱锥的体积为V₁，正方体体积为V₂，且V₁=kV₂，则实数k的最大值为

．

17．如图，三棱柱ABC-A₁B₁C₁中，侧面BB₁C₁C为菱形，B₁C的中点为O，AC=AB₁．

（1）文字叙述平面与平面垂直判定定理；
（2）求证：平面ABO⊥平面ACB₁．

18．在△ABC中，角A，B，C的对边分别为a,b,c,已知
（
a
+
b
）
（
sin
A
-
sin
B
）
=
（
3
a
-
c
）
sin
C
．
（1）求角B；
（2）若
C
=
2
π
3
，
a
=
3
，求BC边上中线的长．

21．已知向量
a
=
（
2
，
1
）
，
b
=
（
sinα
，
2
cosα
）
．
（1）若
α
=
3
π
4
，求证：
a
⊥
b
；
（2）若向量
a
，
b
共线，求tanα．