2022-2023学年江苏省泰州市兴化市九年级（下）第四次素养提升数学试卷（A卷）

一、填空题（每小题5分，共25分）

• 1．如图是2022年杭州亚运会徽标的示意图，若AO=5，BO=2，∠AOD=120°，则阴影部分面积为

  ．
  
  组卷：247引用：4难度：0.7

  解析

• 2．在一个不透明的袋子中有5个除颜色外完全相同的小球，其中绿球2个，红球3个，摸出一个球不放回，混合均匀后再摸出一个球，两次都摸到红球的概率是

  ．
  组卷：1425引用：8难度：0.3

  解析

• 3．我国古代数学名著《四元玉鉴》中记载：“九百九十九文钱，及时梨果买一千，一十一文梨九个，七枚果子四文钱．问梨果各几何？”意思是：用999文钱买得梨和果共1000个，梨11文买9个，果4文买7个，问梨果各买了多少个？如果设梨买x个，果买y个，那么可列方程组为

  ．
  组卷：57引用：3难度：0.7

  解析

• 4．魏晋时期，数学家刘徽利用如图所示的“青朱出入图”证明了勾股定理，其中四边形ABCD、四边形EFGD和四边形EAIH都是正方形．如果图中△EMH与△DMI的面积比为

  16

  9

  ，那么tan∠GDC的值为

  ．
  组卷：464引用：5难度：0.6

  解析

二、解答题（本大题共7小题，共75分）

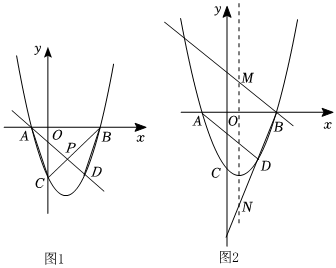• 11．如图1，抛物线y=ax²+bx-3（a＞0）交x轴于点A，B（点A在点B左侧），交y轴于点C，且OB=OC=3OA，点D为抛物线上第四象限的动点．
  （1）求抛物线的解析式．
  （2）如图1，直线AD交BC于点P，连接AC，BD，若△ACP和△BDP的面积分别为S₁和S₂，当S₁-S₂的值最小时，求直线AD的解析式．
  （3）如图2，直线BD交抛物线的对称轴于点N，过点B作AD的平行线交抛物线的对称轴于点M，当点D运动时，线段MN的长度是否会改变？若不变，求出其值；若变化，求出其变化的范围．
  组卷：598引用：4难度：0.4

  解析

• 12．如图1，在正方形ABCD中，P是边BC上的动点，E在△ABP的外接圆上，且位于正方形ABCD的内部，EA=EP，连结AE，EP．
  （1）求证：△PAE是等腰直角三角形；
  （2）如图2，连结DE，过点E作EF⊥BC于点F，请探究线段DE与PF的数量关系，并说明理由；
  （3）当点P是BC的中点时，DE=4．
  ①求BC的长；
  ②若点Q是△ABP外接圆上的动点，且位于正方形ABCD的外部，连结AQ．当∠PAQ与△ADE的一个内角相等时，求所有满足条件的AQ的长．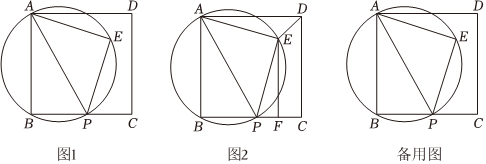
  
  组卷：289引用：3难度：0.5

  解析